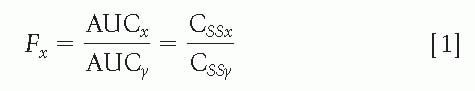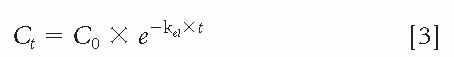Pharmacokinetics and Pharmacodynamics of Antiepileptic Drugs
Blaise F. D. Bourgeois
The principles of pharmacokinetics and pharmacodynamics are heavily rooted in mathematics and may, at first, appear far removed from clinical practice. However, these disciplines of pharmacology provide powerful tools for the optimal use of antiepileptic and other drugs. Pharmacokinetics refers to drug concentrations in the body and their changes over time as a function of absorption, distribution, and elimination (what the body does to the drug). Pharmacodynamics describes the action of drugs (what the drug does to the body), especially in the target organ. Many who study these concepts do not routinely treat patients, and many involved in patient care tend to regard these concepts as less-than-useful tools for everyday clinical practice. In an effort to bridge these gaps, this chapter emphasizes the practical relevance of pharmacokinetic and pharmacodynamic principles to the treatment of patients with epilepsy.
BASIC PHARMACOKINETIC PARAMETERS
Only five or six pharmacokinetic parameters determine the blood level of a drug in a patient at any given time following a single or repeated dose by any route of administration. This concentration is a function only of extent and rate of absorption, distribution within the body, and rate of conversion or elimination (Table 45.1). Table 45.2 summarizes the main pharmacokinetic parameters, and Table 45.3 summarizes the recommended therapeutic ranges and average doses of several commonly used benzodiazepines and antiepileptic drugs (AEDs).
Absorption Parameters
Bioavailability
The amount of an administered dose that will reach the bloodstream, that is, bioavailability (F) for fraction, is a function of the route of administration and the drug preparation. Bioavailability becomes an issue in clinical practice only when one of these factors is changed, and knowing the relative bioavailability of a drug may be important. After intravenous (IV) administration, bioavailability is 1, or 100%. The absolute bioavailability can be calculated by comparing IV absorption with the absorption of a drug by any other route. If a drug cannot be administered intravenously, the relative bioavailability of two routes or two preparations can be calculated; this is often sufficient for clinical purposes. Bioavailability is usually determined by calculating the surface under the drug concentration-versus-time curve, that is, the area under the curve (AUC), following a single dose by two different routes, x and y, or for preparations x and y of the same drug, according to the following equation:
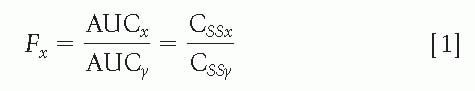
A correction is necessary if the doses for x and y are different. This equation also shows that F can be estimated by comparing steady-state concentrations (CSS), a less precise method, because CSS fluctuates throughout the day according to drug intake; and even if obtained at the same time of day, CSS values are less reproducible than is the AUC. In addition, steady-state conditions must be achieved for both preparations or both routes, which can be impractical with IV or rectal administration.
|
TABLE 45.1 PHARMACOKINETIC PARAMETERS | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
An example of bioavailability determination for different routes of administration is provided by a study (1) in which the relative bioavailability of sodium valproate was calculated for the oral solution, enteric-coated tablets, and suppositories by comparing AUCs over 24 hours at steady state. Bioavailability was similar for the three preparations, and only absorption rates differed. A comparison between different galenic preparations of the same drug, with CSS used as a measure of bioavailability, is found in a report (2) on decreasing levels of primidone after the trademark product was replaced by the generic form. The levels returned to their initial values after reintroduction of the proprietary product. Unlike other AEDs, gabapentin has saturable dose-related bioavailability. As single doses increase, bioavailability can decrease from 60% to 30% (3). This may require fractionated four-times-daily administration at high doses.
|
TABLE 45.2 PHARMACOKINETIC PARAMETERS OF ANTIEPILEPTIC DRUGS | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Absorption Rate
Although the rate of absorption receives less attention from clinicians than do elimination parameters, it is just as important for optimal patient management, and the kinetic principles are the same for both. Absorption is generally a first-order (or exponential) process with a half-life, or constant (kabs), that is the equivalent of the elimination constant (kel). Rapid absorption is desirable when a rapid effect is necessary but is usually undesirable during longterm therapy, because it accentuates fluctuations in concentration and necessitates shorter dosage intervals with smaller doses. Ideally, every AEDs should be available as a parenteral solution for IV administration and as a slow-release preparation for long-term use. The slow-release form is not necessary if the agent has a very long elimination half-life (t½), as does phenobarbital.
|
TABLE 45.3 PHARMACOKINETIC PARAMETERS OF BENZODIAZEPINES | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
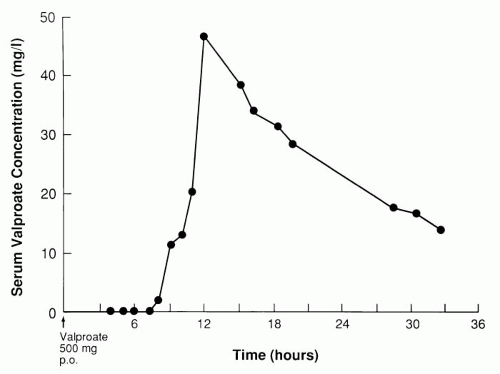
A common misconception is that the enteric-coated form of sodium valproate, or divalproex sodium, is a slow-release preparation. Enteric-coated valproate is not absorbed before it reaches the small intestine, but once the gastricresistant coating has been dissolved, absorption is rapid. Figure 45.1 shows serum levels of valproate after a single, first oral dose with a meal. For up to 7 hours after oral intake, valproate was not detectable in the blood, but absorption proceeded rapidly thereafter. This concentration curve indicated a delayed but fast absorption, whereas the slow-release preparations are absorbed slowly. Because of this delayed absorption of enteric-coated valproate, the lowest serum concentration of the day during long-term intake is not before the first morning dose, but usually around noon or early afternoon (1). Consequently, the morning “trough” level is a misnomer. This does not apply to the enteric-coated sprinkle capsules of divalproex sodium.
Figure 45.1 Serum concentrations of valproate after a 500-mg single, first oral dose of enteric-coated divalproex sodium in a 60.4-kg woman. The medication was taken with a meal. |
Distribution Parameters
Once a drug reaches the blood, regardless of the route of administration, it will diffuse into other body fluids and various tissues until an equilibrium is reached. The extent of distribution is expressed by the volume of distribution (Vd), which often has no anatomic boundaries. The Vd is the hypothetical volume whose calculation is based on the assumption that drug concentration equals concentration in blood plasma throughout this volume (often not the case). Thus, Vd can be determined by dividing the IV dose (DIV) by the increase in blood level (ΔC) associated with this dose. This is the same as the total amount of drug in the body (Q) divided by the blood concentration (C):
The Vd is usually expressed as a relative value in liters per kilogram. In a 70-kg adult, a relative Vd of 0.5 L/kg corresponds to an absolute Vd of 35 L. Because body water represents approximately 60% of body weight, a drug with a Vd >0.6 L/kg must be assumed to be bound to certain tissue components. A decrease in serum protein binding can result in a higher value for Vd, which is based on total serum levels. Moreover, depending on the affinity of a drug for adipose tissue, Vd (L/kg) can be larger or smaller in obese individuals.
Although Vd is a theoretical concept, it has practical clinical usefulness by providing the ratio necessary to calculate the dose to load a patient rapidly to a desired blood level. Equation 2 can be solved for the dose (D = Vd × ΔC) or for the concentration (ΔC = D/Vd). For example, an IV dose of 18 to 20 mg/kg phenytoin or phenobarbital is the standard treatment for status epilepticus. Because the Vd of phenytoin is about 0.75 L/kg, the concentration after the infusion will be 20/0.75 = 26.7 mg/L—adequate for a peak concentration. The Vd of phenobarbital is approximately 0.55 L/kg, yielding a peak concentration of 20/0.55 = 36.4 mg/L.
The dose for reloading to a desired level can also be calculated. Let us assume that the phenytoin level is 15 mg/L and the desired level is 25 mg/L. The necessary dose will be (25 − 15) × 0.75 = 7.5 mg/kg. In nonurgent situations, loading with a drug need not be limited to the IV route and can be extended over any length of time; however, the desired level will be attained only if the maintenance dose for this level is given in addition to the loading dose during the loading period.
For example, let us assume that a 67-kg adult is estimated to require a phenytoin maintenance dose of 400 mg per day, or 6 mg/kg, to achieve a steady-state level of 18 mg/L. The patient has not yet received any phenytoin, and the goal is to reach a level of about 18 mg/L within 48 hours. This will be achieved if the patient receives a loading dose of 67 × 0.75 × 18 = 904.5 mg + 800 mg, the latter being the maintenance dose for 48 hours. The total dose of approximately 1700 mg can be spread evenly over 48 hours: three 300-mg doses the first day, and 300 mg, 300 mg, and 200 mg the second day. Administering only the 900-mg loading dose over 2 days will yield a level well below 18 mg/L, because during that time, elimination of phenytoin by the liver will be ongoing.
If the final concentration equilibrium of a drug is reached rapidly following IV administration, distribution is said to occur according to a one-compartment model. If, however, a drug is rapidly distributed into one compartment but then slowly diffuses into a second and even a third compartment, distribution occurs according to a two-or three-compartment model. The total Vd will correspond to the sum of these two or three compartments. After a single IV injection, biexponential or triexponential decrease of the blood concentration will occur. Under steady-state conditions, the serum concentrations will be determined by the total, or largest, Vd; the distinction between two or three different Vd values is usually of little importance. An exception is during rapid administration and loading, because the Vd will initially be small and will increase with time. This will require repeated administration of the agent to maintain a given blood level.
Figure 45.2 Linear elimination kinetics in a two-compartment model. A: Concentration and time on a linear scale; (B) concentration on a logarithmic scale. α, slope of the distribution phase; β, slope of the elimination phase, which is equal to kel, elimination constant. |
The rate at which a drug diffuses into the second or third compartment is usually expressed as the distribution half-life, or distribution constant α, as opposed to the elimination half-life, or elimination constant β. This distinction is discussed in the section “Elimination Parameters.” A classic example of a two-compartment model is diazepam, which is commonly administered intravenously in patients with status epilepticus. Blood levels of diazepam decrease rapidly under these circumstances, with a half-life of 1 hour or less. This is actually a distribution half-life; the true t½ of diazepam is about 36 hours.
Elimination Parameters
As soon as a drug is present in circulating blood, elimination from the bloodstream begins via enzymatic biotransformation in the liver, directly by the kidneys in an unmetabolized form, or through both processes. This elimination is clinically important because it determines both the rate at which the drug concentration will decrease once absorption is complete and the rate at which the drug will need to be replaced if a certain concentration is to be maintained.
Linear Elimination Kinetics
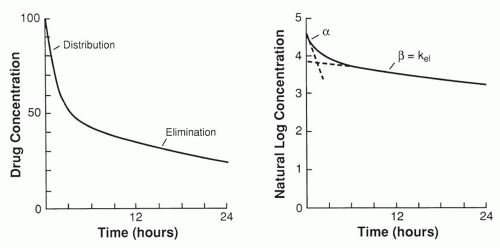
For most drugs, elimination is said to follow linear kinetics, which means that all processes occur in a linearly proportional fashion. For example, the number of drug molecules that will circulate through the liver or the kidneys will be twice as high for a blood concentration of 20 mg/L as for one of 10 mg/L; consequently, per unit of time, twice as many drug molecules will be metabolized by hepatic enzymes or filtrated by glomeruli at 20 mg/L as at 10 mg/L. This also means that the blood concentration will decrease twice as fast at 20mg/L as at 10 mg/L, resulting in an exponential decay curve for the drug concentration or a linear fall if the concentration is plotted on a logarithmic scale (Fig. 45.2). The slope of the second straight segment in Figure 45.2B is called β, or elimination constant kel. Its units are usually hours−1 or 1/hour, and it represents the fraction of drug eliminated per hour, this fraction being constant by definition. The half-life of the drug can be calculated from the value of kel, the relationship being t½ = ln 2/kel = 0.693/k el.
Following IV administration, the concentration (Ct) as a function of time is
in which C0 is the concentration at time 0 following the IV administration.
Although the basic pharmacokinetic elimination parameter is kel, the concept of half-life is more useful clinically and helps to determine (a) how long it will take for a concentration to decrease from 40 to 20, from 20 to 10, or from 10 to 5; (b) how often the agent needs to be administered during long-term treatment (if possible, at least once every half-life); and (c) how long before steady-state levels are reached if the drug is introduced at a constant daily dose. The slope of the first straight segment in Figure 45.2B is the distribution constant α. With the use of this slope, the distribution half-life can be calculated as ln 2/α by means of Equation 3. Drugs with rapid distribution into one compartment have a negligible distribution half-life. As discussed, drug absorption is most often a first-order process. If absorption is regarded as a linear elimination from the intestinal lumen, the same concept can be used as for elimination (Fig. 45.2), resulting in an absorption constant (kabs) and an absorption half-life. The absorption half-life can be calculated only indirectly, because absorption and elimination always occur simultaneously, whereas elimination can occur alone once absorption is complete.
Nonlinear Elimination Kinetics
As noted, at a concentration of 20 mg/L, twice as many drug molecules will circulate through the liver per unit of time, and twice as many molecules will undergo enzymatic biotransformation as at a concentration of 10 mg/L. This is true as long as the corresponding enzymes are not becoming saturated and can continue to bind additional drug molecules. Phenytoin differs from other AEDs in that the enzymes responsible for most of its elimination are already partially saturated at concentrations within the recommended therapeutic range. As the concentration increases, the enzymes will no longer be able to increase the rate of biotransformation proportionally, and the linear kinetic model will no longer apply. The kinetics are now called concentration-dependent, or saturable, and there is no true half-life because the time required for the concentration to decrease by 50% of its value becomes progressively longer at higher concentrations. Steady-state levels of phenytoin increase disproportionately as the maintenance dose is increased.
The kinetics of enzymatic activity have been elucidated in vitro by biochemists, and no attempt will be made to elaborate on this theory. The parameters, however, can be translated into simple clinical concepts useful in the daily routine. Let us consider the patient’s Vd as a huge test tube and the liver as the enzymes in the test tube that are involved in phenytoin biotransformation. Every patient has a given number of enzyme molecules in his or her liver that become progressively saturated as the phenytoin concentration increases. The patient’s maximal reaction velocity (Vmax) is reached when all enzyme molecules are continuously saturated and working at maximal capacity. Theoretically, this state of saturation is attained only at an infinitely high drug concentration. Maximum reaction velocity is not an abstract concept, but can be expressed in milligrams per day or milligrams per kilogram per day. Average adult values for Vmax of phenytoin are about 8 mg/kg per day; this means that the liver of a normal 70-kg patient cannot metabolize more than about 560 mg phenytoin per 20 hours. If the patient ingests 600 mg per day, each day’s drug intake will exceed the elimination rate, and at least 40 mg, or 0.57 mg/kg, will accumulate. With an assumed Vd of 0.75 L/kg and with the use of Equation 1, the patient’s blood level will increase indefinitely by at least 0.76 mg/L every day for as long as this dose is taken. This relatively small, yet persistent increase may be overlooked for a few days, but will invariably result in toxic levels after 1 week or less than 1 month. The maintenance dose should always be lower than the Vmax.
The second parameter for saturable kinetics is the Michaelis constant (Km)—the blood level at which one-half of Vmax is reached. For phenytoin, the average value in adult or pediatric patients is about 6 mg/L, or 6 μg/mL. The Km reflects the binding affinity between the enzyme and the drug, and its value is inversely proportional to this affinity. How Vmax and Km can be used to calculate dose requirements or to predict a steady-state level at a given dose is discussed in the next section.
STEADY STATE AND CLEARANCE
When a drug is introduced at a constant daily dose, the levels initially will be low, the amount eliminated per day will be smaller than the daily dose, and the drug concentration will increase. As concentration increases, so does elimination, until it equals the daily maintenance dose. This final concentration is the CSS. The maintenance dose is best viewed as the daily replacement dose necessary to match drug elimination and thus maintain CSS. At a constant daily dose, 97% of CSS is reached after five elimination half-lives of the drug. Because antiepileptic therapy is longterm in most patients, steady-state levels are particularly important in therapeutic monitoring. For any drug with linear elimination kinetics, the ratio between maintenance dose (or dose per unit of time, D/t) and the CSS is constant and is equal to the clearance (Cl):
Far from being an abstract entity, clearance is probably the most clinically relevant parameter in long-term antiepileptic therapy. This ratio indicates the maintenance dose necessary to achieve a desired level, as well as the expected level at a given D/t. It can be calculated by turning Equation 4 around:
It is best to express D/t in milligrams per kilogram per day, CSS in milligrams per liter, and clearance in liters per kilogram per day. Drug clearance does not differ from creatinine clearance (24-hour urinary creatinine excretion/plasma creatinine). Plasma creatinine is a steady-state level, and 24-hour urinary excretion of creatinine is the equivalent of the maintenance (replacement) dose.
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
