(1)
Asheville, NC, USA
By the early 1900s proteins had been studied for more than a hundred years. Chemists had begun to extract proteins such as albumin and wheat gluten from animals and plants at the beginning of the previous century. The Dutch chemist Gerardus Johannes Mulder (1802–1880) had found that each one of these proteins had nearly the same composition. He thought that all were variations on a single primordial substance composed of carbon, nitrogen, hydrogen, and oxygen with variable amounts of sulfur and phosphorus. In 1838, the Swedish chemist Jöns Jacob Berzelius (1779–1848) coined the name “protein” for this universal substance. These events were followed by groundbreaking investigations carried out in the later 1850s and 1860s by August Kekulé (1829–1896) that helped lay the foundations for structural chemistry and protein science. In his studies, Kekulé uncovered the tetravalent character of carbon, proposed its ability to bond to other carbons in long chains, and discovered the ring structure of benzene.
That proteins were enormous molecules was recognized right at the start. The molecular structure deduced by Mulder, C400H620N100O120P1S1, was far larger than any other molecules studied at that time. In order to better understand its structure and composition, proteins were hydrolyzed with dilute acids or bases, and the breakdown products analyzed. By this means (or similar ones), the 20 amino acid constituents of proteins were discovered one by one over a period of time that stretched from 1819 (leucine) to 1936 (threonine). These efforts culminated in 1902 (by then 16 of the 20 amino acids had been correctly identified). In that year, the central concept that proteins are linear chains of amino acids held together by peptide bonds was put forth simultaneously by Emil Fischer (1852–1919) and Franz Hofmeister (1850–1922), Fisher having coined the term peptide bond to describe the linkage.
One of the chief properties that interested early protein scientists was the ability of proteins such as albumins, globulins, and hemoglobin to coagulate when subjected to heating. Harriette Chick (1875–1977) was a well-known British nutritionist, biochemist and one of the first protein scientists. She and Lister Institute director Charles Martin (1866–1955) published a series of papers from 1910 to 1912 in which they established that there were two distinct steps in the “heat coagulation” (their quotes) of egg albumin and hemoglobin. The first step was that of denaturation and this step was separate from the second precipitation step that depended on pH and salts but not heat. These findings established denaturation as a distinct process that altered the functional properties of the proteins, resulting in their loss of catalytic ability, for example.
Among the people studying the responses of proteins to changes in temperature, pH, and salts was the Chinese protein scientist and founder of modern Chinese biochemistry Hsien Wu (1893–1959). In 1931, he became the first to recognize that protein denaturation was a process in which protein underwent a conformational change. During this same time period—from 1925 to 1936—denaturation of a variety of proteins was examined by several groups. In a 1925 paper, Mortimer Louis Anson (1901–1968) and Alfred Mirsky (1900–1974) reported that the unfolding of hemoglobin was reversible. This result was an exceptionally significant one and was tested with other proteins. It was found to be not unique to hemoglobin but rather other proteins such as trypsin could be reversibly unfolded and then refolded as well. However, egg albumin could not. Its importance was conveyed to a broad audience by Alfred Mirsky and Linus Pauling (1901–1994) in a 1936 paper entitled “On the structure of native, denatured, and coagulated proteins”, and by Max Perutz (1914–2002) through a 1940 popular presentation entitled “Unboiling an Egg”.
The chapter will begin as it must with the discovery of the alpha helix (Fig. 2.1) and beta sheet by Pauling, Robert Brainard Corey (1897–1971), and Herman Russell Branson (1914–1995), and with the discovery of the 3D protein structures of myoglobin and hemoglobin by John Cowdery Kendrew (1917–1997) and Perutz. It will then resume the discussion of denaturation and reversibility with the most famous of the denaturation/reversibility experiments—those of Christian B. Anfinsen (1916–1995)—leading to his thermodynamic hypothesis .


Fig. 2.1
Linus Pauling and Robert Corey in 1951 with their model of the alpha helix, Courtesy of the Archives, California Institute of Technology
2.1 Discovery of the Alpha Helix and Beta Sheet
The discovery of the alpha helix and beta sheet by Pauling, Corey, and Branson was a seminal event. In a series of eight articles appearing in the Proceedings of the National Academy of Sciences in early 1951, they described the forms that these preeminent structures should take and their stabilization by hydrogen bonds between amide (NH) and carbonyl (CO) groups. In alpha helices, the hydrogen bonds form between a carbonyl group on the ith residue and the amide group on the (i + 4)th residue lying below it. In beta sheets, the hydrogen bonds form between carbonyl group lying on one strand and the amide group situated immediately adjacent to it on another strand. The beta strands can be oriented in either a parallel or an antiparallel manner.
In the alpha helix, the backbone forms the inner portion of structure while the side chains rotate outward. Alpha helices are about ten residues in length and these structures account for about a third of the amino acid residues in a typical protein. Individual beta strands are typically six amino acid residues in length and they account for a quarter of the residues. Turns allow the chain to reverse direction. They along with loops are usually located on the protein surface.
A number of essential ingredients entered into their search for the two repeating hydrogen-bonded structures. The first component was the need for precisely determined bond strengths and bond angles. That was determined in previous work. The second ingredient was one that was missed in previous attempts to find these regular structures. That was the observation that the N–C peptide bond was partially double in character and therefore quite rigid. That point is illustrated in Fig. 2.2 showing that the six atoms are roughly coplanar leaving the only degrees of freedom represented by the two torsion angles, φ and ψ.
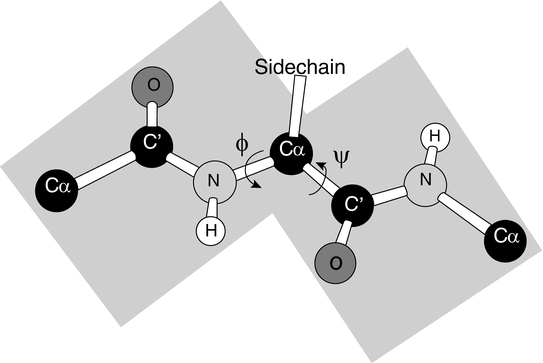

Fig. 2.2
The planar peptide bond and associated torsion (rotation) angles φ and ψ (from Rose PNAS 103: 16623 © 2006 National Academy of Sciences, U.S.A. and reprinted with their permission)
The third component was that of steric constraints, namely, two molecules cannot occupy the same position in space. These constraints limit the angular regions available for peptide bonding. A primary tool for visualizing these constraints and revealing the underlying structure of the polypeptide chain is the Ramachandran plot, a tool developed in 1963 by the Indian physicist Gopalasamudram Narayana Ramachandran (1922–2001). A pair of these plots is presented in Fig. 2.3.
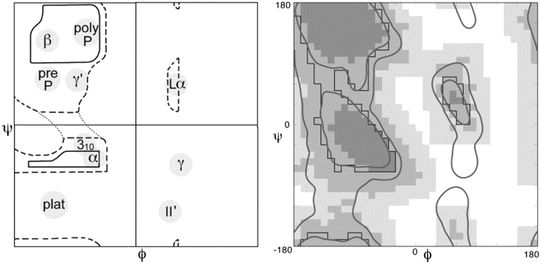

Fig. 2.3
A pair of Ramachandran plots. Not all values of ψ and φ are allowed due to steric constraints. Shown in the left panel is an annotated plot of the allowed ψ and φ values as first presented by Ramachandran. Depicted in the right panel is a refined and updated Ramachandran plot. In this diagram, the darkest shading indicates which areas have high probability of being occupied and by progressively lighter shading those regions that might still be occupied but with lower probability as determined from the data. The large empty regions correspond to (ψ, φ) values that are sterically forbidden. The annotations to the left panel highlight the presence of three broad regions populated by alpha helices (α), left-handed helices (Lα) and beta sheet (β), plus several smaller areas (from Lovell Proteins 50: 437 © 2003 John Wiley and Sons, and reprinted with their permission)
Lastly, they abandoned the idea that there had to be a whole integer number of residues per turn. Instead they came up with two solutions—a 3.7 residue per turn helix and a 5.1 residue per turn helix. Their result of what must be one of the great triumphs of model building in science was the alpha helix and the beta sheet.
2.2 The Birth of Molecular Biology
2.2.1 X-Ray Diffraction and the Double Helix of DNA
The preeminent method for exploring the shape and internal structure of proteins at atomic level detail is X-ray crystallography . The use of X-rays to explore protein structure had its beginnings over a century ago. X-rays were discovered in 1895 by Wilhelm Roentgen (1845–1923) leading to his award of the first Nobel Prize in physics in 1901. A few years later, in 1912, Max von Laue (1879–1960) (along with Paul Knipping and Walter Friedrich) discovered that crystals could act as a diffraction grating for the scattering of X-rays. This discovery was immediately followed in by those of William Lawrence Bragg (1890–1971) and his father William Henry Bragg (1862–1942) that established the fundamental relationship between X-ray diffraction patterns and atomic positions in a crystal known as Bragg’s law (see Appendix 1). These pioneering studies focused on simple crystals such as ZnS (von Laue) and NaCl (the Braggs). Using this new physics technique the Braggs made the important finding that atoms of salt are not organized as a molecule but rather as ions and the monumental discovery (along with Laue) of the wavelike properties of X-rays.
These discoveries led to the award of the Nobel Prize in Physics to Laue in 1914 and to the Bragg’s in 1915. WL Bragg was 25 at the time, the youngest-ever recipient of the Nobel Prize in Physics. It is worthwhile to note the role that technology played in making the discoveries by the Bragg’s possible. These breakthroughs could not have been made without being preceded by development of (1) the capability to produce high potency (high voltage) electricity, and (2) the ability to generate high vacuum, plus (3) the invention of dry-plate photography.
Moving forward in time, the extension of X-ray diffraction techniques to large or even moderate biomolecules was regarded by many as impractical if not outright impossible. In spite of these misgivings, efforts to do so began in the 1920s and 1930s with the pioneering studies of fibrous materials such as wool by William Astbury (1898–1961). He had studied in the Bragg’s laboratory and then moved to Leeds, the center of the British textiles industry. At Leeds he successfully carried out X-ray diffraction studies of fibrous materials including keratin (the material out of which wool is made). He was the first to propose that protein chains could be stabilized by forming hydrogen bonds, and proposed that the fibers formed a helix that uncoiled when the fibers were stretched. In doing so, he laid the foundation for the discovery of the alpha helix by Pauling and Corey. His insights into the physics of wool were immortalized in a limerick by A.L. Patterson and presented at the beginning of a 1938 paper by Astbury entitled “X-ray adventures among the proteins”:
Amino-acids in chains
Are the cause, so the x-ray explains,
Of the stretching of wool
And its strength when you pull,
And show why it shrinks when it rains
Astbury also carried out early studies of DNA together with his student Florence Bell. It was already known that chromosomes contain both proteins and nucleic acids. However, at that time DNA was regarded as being too simple a molecule to be the repository of genetic information. Instead, the far more interesting and complex proteins had to be responsible for the storage, with the linear and simpler DNA merely serving in a structural capacity. Astbury and Bell found that purine and pyrimidine bases were stacked along the axis of the molecule, but the full analysis had to wait for Crick and Watson and the X-ray diffraction studies of DNA by Maurice Hugh Frederick Wilkins (1916–2004) and Rosalind Elsie Franklin (1920–1958) in which the existence of two distinct structural forms was first made apparent. The missing ingredients to finding the structure were then supplied by Crick and Watson using the new data. In arriving at their famous solution, they had to get past the prevalent notion at the time of simple crystalline solid arrangements. In their place, they followed Pauling and Corey and introduced helices with nonrational number of repeating units per 360° turn. Finally, they made the great leap forward by proposing the complementary base-paired, double helix that no one before had thought of. Once that structure had emerged it became apparent that is could serve as the information storage. That conclusion appeared, in one of the greatest understatements of science, as a single sentence near the end of their brief two-page paper announcing their discovery of the structure of DNA:
It has not escaped out notice that the specific pairing we have postulated immediately suggests a possible copying mechanism for the genetic material.
2.2.2 The First Protein Structures Are Solved by Kendrew and Perutz
The first clear picture of what a protein looks like in three dimensions was presented by John Kendrew (1917–1997) in 1958 with his publication in Nature of the crystal structure of myoglobin. This landmark event was followed in 1960 with the publication of a more refined myoglobin structure by Kendrew and with the publication also in Nature by Max Perutz (1914–2002) of the three-dimensional structure of hemoglobin. These efforts had their antecedents in the earlier work of Astbury discussed above and also in a study by John Desmond Bernal (1901–1971) and his student at the time, Dorothy Crowfoot Hodgkin (1910–1994). They obtained the first X-ray diffraction picture of a nonfibrous protein, pepsin, and published their results in 1934 in Nature. That effort served as inspiration for Perutz who had joined Bernal at Cambridge in 1936.
The fundamental challenge faced by Perutz and others with solving the three-dimensional structure of a complex biomolecule from X-ray diffraction data is known as the “phase problem”. In order to extract electron densities from the patterns of light and dark spots, one needs to know not only the positions and intensities of the light spots but also its phases. This is not contained in the data. For small molecules one can use additional information and guesswork to overcome the phase problem, but this approach becomes progressively more difficult to execute as the number of atoms in a unit cell increases. This necessitates the development of alternative methods that compensate for the missing phase information. Perutz created one of these methods, known as isomorphous replacement, to solve the phase problem. In his approach, heavy atoms (having many more electrons than the atoms of the biomolecule) are added to the protein of interest without altering the crystal formation (hence the appellation “isomorphous”). The additional atoms do not shift the locations of the light and dark spots but do alter their intensities. From the patterns with and without the heavy atoms enough information is now present to extract the needed phases.
The solution found by Perutz involved attaching mercury atoms to the hemoglobins in a way that left the locations of the spots alone while changing the intensities. That method was published in a pair of papers that appeared in 1954. The second crucial innovation utilized by Perutz was that of a Patterson map, an inventive way of using just the intensities to produce a map of the relative positions of pairs of atoms in the structure. That crucial intermediate step was pioneered in 1934 by Arthur Lindo Patterson (1902–1966).
When the 3D protein structures were finally solved (Fig. 2.4) the responses throughout the field were surprise (and perhaps dismay) at the complexity and lack of any obvious order to the arrangement of amino acid residues. Pauling’s alpha helices were clearly present in the crystal structures but these were arranged in ways that were not even remotely obvious. That response to the structure was best summarized by Kendrew in his 1958 publication in Nature:

Fig. 2.4
The structure of myoglobin at 6 Å resolution solved by Kendrew in 1958. Presented in this figure is a high res reconstruction of the original Kendrew drawing from his 1958 Nature article (from Fersht Nat. Rev. Mol. Cell Biol. 9: 650 © 2008 Reprinted by permission from Macmillan Publishers Ltd)
Perhaps the most remarkable features of the molecule are its complexity and its lack of symmetry. The arrangement seems to be almost totally lacking in the kind of regularities which one instinctively anticipates, and is more complicated than has been predicted by any theory of protein structure.
2.3 Anfinsen’s Postulate and Thermodynamic Hypothesis
2.3.1 The Divide Between Chemistry and Biology Is Breached
In 1969, at a joint press conference, two groups reported that they had successfully synthesized an enzyme, ribonuclease A, composed of 124 amino acids. One team situated at Merck Research Laboratory was led by Ralph Franz Hirschmann (1922–2009) and the other located at Rockefeller University was headed by Robert Bruce Merrifield (1921–2006). These researchers solved the previously thought insurmountable problem of how to construct in the laboratory a linear chain of amino acids in the correct fashion to make a biologically viable protein given that each amino acid has multiple binding sites and only one of these in each instance is the correct one. These efforts were following in 1971 with the publication by Merrifield of a paper reporting that the linear sequence of amino acids joined via peptide bonds can determine by itself the enzyme’s three-dimensional (tertiary) structure. (Merrifield was awarded the Nobel Prize in Chemistry in 1984 for his invention of solid phase peptide synthesis, the method he used to synthesize ribonuclease A.)
2.3.2 Anfinsen’s Postulate
The first and most important set of clues of how a protein folds into its complex shape comes from the denaturation and refolding experiments. The most famous of these experiments are those of Christian Anfinsen (1916–1995). He showed in his studies of ribonuclease that not only can it be made to refold after unfolding even under extreme conditions, but its enzymatic activity will be restored, as well. He then postulated that all the information needed to fold a protein is encoded in its primary amino acid sequence. He further hypothesized that the process of folding and unfolding obeys the laws of thermodynamics, and this assertion has come to be known as the thermodynamic hypothesis . Given that a cell functions far from thermodynamic equilibrium this statement is in itself a remarkable one. These studies took place in the 1950s and early 1960s and led to his being awarded the 1972 Nobel Prize in Chemistry (along with Stanford Moore and William Howard Stein who elucidated the connection between the chemical structure and catalytic activity of ribonuclease).
Thermodynamic stability is an essential property of a protein. To be useful, a protein’s native state must be stable in the thermodynamic sense. Such states, once formed, do not change appreciably in time. The effects of small perturbations and of thermal fluctuations are rapidly damped out and the behavior of the protein is not appreciably altered. These are equilibrium states in the language of thermodynamics. To establish stability in the thermodynamic sense one must show that (1) the native folded conformation is a function of state alone, that is, it does not depend on path or process used to get there, and (2) that the native state is situated at a global minimum in the Gibbs free energy. The reversible unfolding and refolding experiments established that under physiological conditions a protein’s folded (native state) was a well-defined thermodynamic equilibrium state corresponding to a minimum in the Gibbs free energy. Anfinsen’s framing of folding in the language of thermodynamics followed and incorporated the earlier views of Hsien Wu, Tim Anson, Alfred Mirsky, and Linus Pauling.
Recall from basic biochemistry that the change in Gibbs free energy of a chemical process, in this case that of a protein undergoing folding, is:
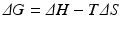
where, ΔH is the change in enthalpy of the system and TΔS is the corresponding change in entropy multiplied by the temperature. Further recall that the enthalpic contribution is the sum of two terms, the change in internal energy of the system, ΔE, plus the amount of work done on the surroundings by the system, pΔV, with ΔV denoting the change in volume and p the pressure (assumed constant). Under the aqueous conditions in which protein folding occurs the pΔV contribution to the enthalpy can be neglected and the change in enthalpy is simply the change in internal energy. The entropic term may be understood in terms of the number of configurations available to the protein at a given energy. As noted by Anfinsen as well as Pauling and many others early on, a denatured protein has many configurations available to it while the native state possesses just a few low energy configurations. Thus, the amount of entropy (disorder) is high when the protein is denatured and low when it is folded tightly into its three-dimensional functional form. This change renders the −TΔS term strongly positive. The condition for a reaction to occur spontaneously is for
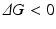
In protein folding this requirement is achieved by the strong negative character of the enthalpic term, that is, through the decrease in internal energy that more than compensates for the opposing entropic contribution.
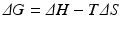
(2.1)
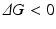
(2.2)
While there are a multitude of states corresponding to the denatured state, there are usually only a few similar states corresponding to the native state and its conformation is essentially unique. In order for the native state to be stable there must be an appreciable gap in energy between the native state and nearby nonnative ones. When the differences are appreciable, it is difficult for small perturbations and thermal fluctuations to induce transitions to the nearby higher energy states. Whenever the energy gaps are small, the proteins will only be marginally stable.
Putting this all together along with the discoveries of messenger RNA and codons results in the central operating principles that guide all of biology along with biochemistry, biophysics, and other related disciplines:
Genetic information is encoded in DNA, which is transcribed into RNA, which is then translated into the protein’s primary sequence.
The primary sequence contains all the information needed to fold the protein into its native-state 3D structure.
The native-state 3D structure determines the cellular function.
2.4 Native-State 3D Structure
Structure-function relationships are of fundamental interest in science. They are the subject of a famous dialog on bone structure (form) written by Galileo Galilei (1564–1642), which appeared in his “Two New Sciences” in 1638. More recently, they played a central role in the classic treatise “On Growth and Form” published in 1919 by D’Arcy Wentworth Thompson (1860–1948). In proteins, the forms of interest are the native-state 3D structures as these determine the physiological function(s) that the protein is capable of performing.
2.4.1 The Protein Structure Hierarchy
There are four basic layers of protein structure—primary, secondary, tertiary, and quaternary. This particular hierarchy of structural elements was introduced by Kaj Ulrik Linderstrøm-Lang (1896–1959) in the Lane medical lectures delivered at Stanford University in 1951 and published in 1952 by the Stanford University Press. The primary structure is simply the covalent structure of the polypeptide chain including any covalent disulfide bonds that form during folding. Its secondary structure refers to the alpha helices and beta sheets that form through hydrogen bonding and turns that connect them. Portions of the polypeptide chain that do not form these regular structures are termed random coil s . As mentioned earlier, alpha helices are typically about ten residues in length while individual beta strands are usually about six residues in length and form hydrogen bonds with other beta strands to form the beta sheets.
It is customary nowadays to add two additional layers in-between the secondary and tertiary structures. Supersecondary structural elements are commonly occurring combinations of secondary structure elements. Examples are the helix-turn-helix and the Greek key (two pairs of antiparallel beta strands). Small supersecondary elements are also referred to as motifs. The other additional structural elements are the domains. These are the chief functional units in the hierarchy of protein structures, and are situated above the secondary and supersecondary structures and below the tertiary structure.
Domains are compact, conserved, three-dimensional parts of a protein capable of carrying out a specific cellular function independently of other parts of the protein. An example of domain structures is presented in Fig. 2.5 in which the 3D native structure of the nonreceptor tyrosine kinase Src is presented. As can be seen in this figure the protein chain folds into several structurally distinct domains. The SH2 (Src-homology-2) and SH3 domains are recognition modules that direct the protein to the correct binding partners. Catalysis is initiated through tyrosine phosphorylation in the activation loop. SH2 domains bind phospholipids and phosphotyrosine-rich sequences such as pYEEI, while SH3 domains bind proline-rich sequences such as PXXP characteristic of PP II helices.
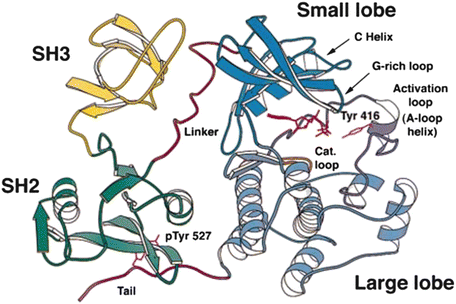

Fig. 2.5
Src domain organization. The amino acid residues in this enzyme are organized into four domains: an N-terminal SH3 domain, a C-terminal SH2 domain, and two catalytic domains connected by a linker sequence (from Xu Mol. Cell 3: 629 © 1999 Reprinted by permission from Elsevier)
Domains such as SH2 and SH3 are highly modular and are found in several hundred proteins. In recognition of the importance of domains, there are several open-access databases devoted to archiving their properties. Two of the most prominent are CATH (Class, Architecture, Topology, and Homology) and SCOP (Structural Classification Of Proteins). The tertiary structure of a protein is its 3D native-state structure. These consist of one or more protein domains. A protein possesses a quaternary structure in those instances where two or more polypeptide chains associate and each folded chain operates as a subunit.
It is customary to represent amino acids that form well-defined secondary structure elements as ribbons. This type of representation was introduced by Jane Richardson in 1981 as a way of converting long list of atomic coordinates determined by means of X-ray crystallography or NMR into something that can be visualized and understood. Since that time, amino acids that form alpha helices have been depicted as coiled ribbons, and those that form beta strands have been shown as flat arrow-like ribbons.
2.4.2 Semi-Independent Folding and Assembly
The picture of a protein constructed in a modular fashion from functionally distinct domains leads naturally to the notion that these structural units may fold independently into their compact tertiary structures. That idea gives rise to the concept of a foldon . These are independent folding units and thus defined through their folding capabilities whereas domains are defined in terms of their functional properties. Ideally, the two ways of defining these crucial structural elements coincide—the independent structural elements fold independently, as well—while allowing that boundaries may vary slightly from one to the other.
One of the most important sets of finding from H/D exchange experiments by Walter Englander (to be discussed in Chap. 3) pertains to the existence of semi-independent cooperative folding by cytochrome c. This protein consists of 103 amino acid residues organized into five foldon units. As uncovered by Englander these units are assembled in a sequential manner during protein folding. Each foldon functions as a cooperative folding entity and the various stages of native structure coalesce out of the random coil one at a time as illustrated in Fig. 2.6. More generally, the notion of stepwise folding and assembly is a common one, and the steps can occur either in parallel or sequentially. A similar theme is present in the zipping and assembly model introduced by Ken Dill in 2007 where small secondary structure elements are formed through hydrophobic zipping (zippering) and these elements then assembly to form the tertiary structure of the protein.

Fig. 2.6
Stepwise assembly of cytochrome c from independent foldons as determined by hydrogen exchange. The various foldons are color coded and assemble in a sequential manner starting with the blue units, then the green units, and next the short yellow connectors, then the red loop, and lastly the nested yellow (white) loop. The protein is depicted covalently-bonded to a heme group (from Maity J. Mol. Biol. 343: 223 © 2004 Reprinted by permission from Elsevier)
2.5 Hydrogen Bonding, Hydrophobic “Forces”, and Steric Constraints Direct Protein Folding
So, how does a protein fold? The answer is that the folding of a protein from an open largely unstructured conformation into a compact 3D native shape is directed by macromolecular force s . The three main contributors are hydrogen bonding, the hydrophobic effect , and steric constrains. Hydrogen bonding is especially important for the formation of secondary structures—the alpha helix and beta sheet. The importance of this driving force was amply illustrated by Mirsky, Pauling, and Corey, and by numerous studies carried out since then. These secondary structures account for the vast majority of hydrogen bonds in a protein. In general, hydrogen bond strengths depend on the partner characteristics and microenvironment conditions under which the residues undergoing hydrogen bonding are operating—polar or nonpolar, or charged or hydrophobic, or solvent-exposed. Bond strengths span a broad range from −0.5 to −4.5 kcal/mol., and average about −1.3 to −1.5 kcal/mol.
The hydrophobic effect is the other major contributor. Walter Kauzmann (1916–2009) championed its importance in protein folding in a famous 1959 review article. In that paper, he noted that during protein folding hydrophobic residues are brought into the interior of the structure, that is, they are buried in the interior, while hydrophilic ones are exposed to the solvent. A short time later Charles Tanford (1921–2009) concluded that the stability of the native conformation was entirely due to the hydrophobic effect. This aspect is still under investigation; an emerging consensus is that Tanford’s assertion is perhaps too strong. A recent estimate is that the two types of forces contribute to protein folding in roughly a 60–40 split, with 60 % coming from the hydrophobic effect and 40 % from hydrogen bonding. The magnitude of these contributions varies somewhat with protein size. Small proteins cannot bury their hydrophobic residues as completely as can large proteins. As a result the hydrophobic contribution is reduced in small proteins.
Just what is the hydrophobic effect ? To answer that question it is worthwhile to consider what happens when oil and water come into contact. That water and oil do not mix has been known for a long time. The phenomenon whereby pouring oil on water stills wave motion was remarked on by Pliny the Elder (AD 23–AD 79). That same phenomenon was studied scientifically many years later by Benjamin Franklin (1706–1790). A century after Franklin, Lord Rayleigh (1842–1919) exploited the phenomenon in his estimation of molecular sizes. The relevance of hydrophobic behavior for proteins was recognized early on by the X-ray crystallography pioneer John Bernal (1901–1971) and in the Nobel-Prize winning studies of oil films by the surface chemist Irving Langmuir (1881–1957).
In brief, the hydrophobic effect arises from the propensity of water molecules to form hydrogen bonds with other water molecules. Typically each water molecule forms three or four hydrogen bonds with nearby water molecules. The result is a three-dimensional lattice work of water molecules. A protein consisting as it does of 20 different kinds of amino acids has a far more complex set of interactions with water than does oil. Some amino acids are polar, while others are nonpolar; some have a net charge, others do not. Hydrophilic (water-loving) residues are polar, and can reorient themselves and form bonds with water molecules. Water molecules have a far greater affinity for other water molecule than for nonpolar amino acids, and the latter are therefore referred to as being hydrophobic (water-hating).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree







