(1)
Asheville, NC, USA
In thinking about how a protein might look in its three-dimensional fully folded form, Hsien Wu had envisioned it as forming a crystalline solid composed of repeated folded structural elements. That hope for simplicity by him and everyone else was effectively dashed by the pioneering studies of Kendrew and Perutz. Studies carried out later by Frederic Richards (1925–2009) [who solved the third ever protein structure in 1967, that of ribonuclease S] and others on packing densities confirmed part of Wu’s depiction. There were few if any large voids in the protein interior, and the overall protein densities were indeed consistent with that of an organic compound in the crystalline state, but one without repeating regularities. However, when examined at a finer scale it turns out that the interiors are quite variable in their packing and do not resemble a tightly fit-together jigsaw puzzle so much as a randomly packed sets of nuts and bolts. The packing is; in fact, loose enough to permit a variety of movements.
This chapter will begin with protein motion s and their importance for protein function. That discussion will set the stage for the modern landscape picture of protein folding which will follow. The landscape picture provides a conceptual framework and vocabulary for thinking about, and visualizing, protein folding. It encompasses not only the rapid two-state folding of small globular proteins but also the far slower folding of large multidomain ones and those that misfold and aggregate. Terms such as pathway diffusion and internal friction will find a simple interpretation within this picture as will kinetic control of folding and intermediate states.
Tools are important, and any field of science moves only as fast as its exploratory toolkit allows. In the case of protein folding, the field has advanced through creation of an ever-expanding body of experimental and theoretical/computational methods. This progression began with chemical denaturation techniques used to unfold and refold proteins. It then leapt forward through atomic level X-ray crystallography and NMR methods, and with chemical, spectroscopic, and computational methods that provide glimpses of the transition and intermediate states along the folding pathways. These exploratory tools will be introduced in the second part of this chapter.
3.1 Protein Motions Are Necessary for Protein Function
Proteins are dynamic, and not static, entities. This central fact has been long recognized and appreciated. According to Richard Feynman (1918–1988) proteins “jiggle and wiggle”, while Gregorio Weber (1916–1997) characterizes them in an even more dramatic fashion as “kicking and screaming”. The three-dimensional forms revealed by X-ray crystallography can be thought of as snapshots, frozen in time, of the proteins’ average structure. Proteins undergo constant motions about these average conformations. Proteins motions range from small amplitude low-energy vibrational and rotational motions over femtosecond to nanosecond timescales to large-scale domain movements over a microsecond to second-plus timescales. The amplitudes of the motions vary from 0.01 Å to 100 Å, and their corresponding energies from 0.1 kcal to 100 kcal.
Motions are essential for protein function. In a series of landmark studies, Hans Frauenfelder, Robert Austin and their coworkers explored how motions regulate protein function. The protein examined by them was myoglobin (Mb), the 153 amino acid oxygen-storage protein whose structure was pioneered earlier by Kendrew and Perutz. The goal in the studies by Frauenfelder and Austin was to identify exactly how oxygen storage and release took place. What they found was that the penetration of dioxygen (O2) and carbon monoxide (CO) into the heme binding sites was made possible by the ability of myoglobin to continually undergo small movements and equilibrium fluctuations (EFs). If myoglobin was completely fixed in its shape and unable to move the protein could not function. The picture that emerged was one in which the native and other long-lived states are not single unique conformations but instead consist of ensembles of substates arranged in a hierarchical manner to form an energy landscape . This central aspect of protein structure and function is depicted in Fig. 3.1.
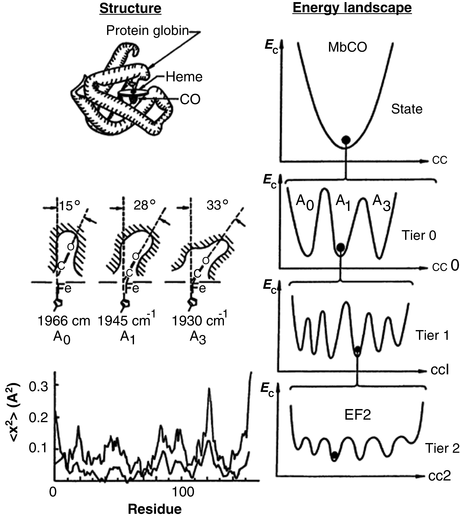

Fig. 3.1
Structure and free energy landscape of MbCO. Left-hand panels: Myoglobin structure. Right-hand panels: Hierarchy of conformational energies (E c) as a function of a conformational coordinate (cc). Illustrated is the treelike arrangement of conformational states and substrates showing the progression from substrates separated by large barriers at the highest tiers to substates separated by small equilibrium fluctuation (EF) barriers at the lowest levels the hierarchy (from Frauenfelder Science 254: 1598 © 1991 Reprinted with permission from AAAS)
3.1.1 Stability Against Perturbations
The most important property of a system in thermal equilibrium is its stability against random perturbations. The theory underlying this stability is summarized by a family of statistical physics findings known collectively as the fluctuation-dissipation theorems. These principles were first stated by Harry Nyquist (1889–1976) in 1928 and later proven by Herbert Callen (1919–1993) and Theodore Welton (1918–2010) in 1951. These theorems establish that the spontaneous fluctuations in a system at equilibrium with its surroundings are indistinguishable from deviations from equilibrium generated by small nonequilibrium perturbations. This happens because the regression (decay) of the spontaneous fluctuations in a system at equilibrium occurs through the same mechanisms that promote the relaxation towards equilibrium of (small) nonequilibrium perturbations in that system.
3.1.2 Motions Beget Function
The connection between motions and function are becoming clearer over time. For example, it has been found that motions enable an enzyme to carry out its function in a folded state in which the catalytic site is often buried, and underlie the ability of a protein to undergo allosteric regulation. In short, internal motions must be considered an intrinsic part of a protein’s native-state 3D structure. They are essential for folding as they “lubricate” the process (to overcome internal friction) and enable escape from the myriad of small barriers that are encountered along the folding pathways no matter how smooth. Shown in Fig. 3.2 is a generalized depiction of a three-tiered, hierarchical arrangement of states and basins, and their substates. The lowest tiers encompass the fast picosecond and nanosecond timescales involved in small amplitude fluctuations—bond vibrations, side chain rotations, and loop motions—while the far slower microsecond, millisecond, and longer timescales are required for large-scale collective motions such as domain movements. This aspect will be discussed in greater detail in Sect. 3.6.
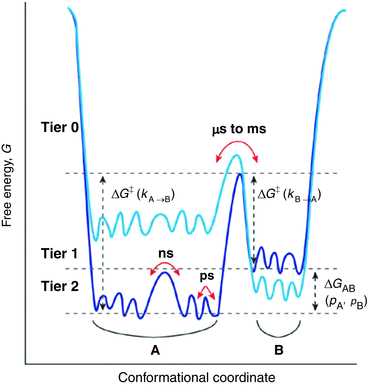

Fig. 3.2
Hierarchical protein motion landscapes. Sates and substates have been arranged in a in three tiers according to the energies, barrier heights, and timescales involved in the states and transitions between them. Transition rates between states are determined by the barrier heights. The changes in color from dark to light blue illustrate how mutations and other actions can alter the relative positions of states A and B in the landscape (from Henzler-Wildman Nature 450: 964 © 2007 Reprinted by permission from Macmillan Publishers Ltd)
3.2 Role of Solvent Fluctuations in Protein Motions
The interactions between proteins and water have been a subject of study for over a hundred years. As early as 1913, Chick and Martin had looked at differences in density and volume between dry and hydrated caseinogen, egg- and serum albumin, and serum globulin. In examining their X-ray images of pepsin, Bernal and Crowfoot reported in 1934 that proteins were “relatively dense globular bodies…separated by relatively large spaces that contain water”. That water filled and remained bound to proteins in solution was demonstrated by a series of measurements for hemoglobin in the 1930s by Gilbert Adair (1896–1979), the discoverer of protein quaternary structure and cooperative binding.
Given that water surrounds and permeates the native state of a protein it is perhaps not too surprising that water influences protein motion s . Protein motion s can be divided into two groups according to the influences of solvent fluctuation s upon them:
Nonslaved motions: These are independent of solvent fluctuation s . These motions are determined by the protein conformation and vibrational dynamics.
Slaved motions, in contrast, are tightly coupled to solvent fluctuation s .
Primary, slow, α-fluctuations in the bulk solvent surrounding and permeating the protein drive and regulate the protein’s first tier, consisting of large-scale motions and changes in conformation. These are controlled by the solvent viscosity.
Secondary, fast, β-fluctuations in the hydration layer drive and regulate the protein’s smaller-scale internal motions taking place in the lower tiers in the hierarchy of protein substates.
3.3 The Energy Landscape Picture
Out of the universe of possible polypeptide chains, evolutionary pressure has sculpted a small number that fold into stable native shapes in physiologically useful times. The folding of these proteins is directed by the macromolecular force s in an energetically downhill fashion satisfying the thermodynamic requirements. These proteins utilize cooperativity (and all the other folding mechanisms discussed in the preceding chapter) in order to avoid becoming stuck in local minima surrounded by barriers too high to permit escape in reasonable time frames.
Proteins fold in ways that do not require exhaustive conformational searches. Instead, they fold along pathways that follow the contours of an energy surface in an overall downhill direction, taking them from an unfolded conformation to their native state. Each point in an energy landscape would represent a possible conformation of the protein. Similar conformations would be found near one another, and dissimilar ones further apart. Each state (point) in the energy landscape represents an ensemble of states and substates representing the intrinsic motions and influences of the solvent at the given temperature.
In this type of representation, the vertical axis denotes the sum of all contributions to the internal or potential energy of the protein while the entropic contribution to the Gibbs free energy is depicted by the width of the energy surface so generated. The horizontal axis itself gives the values of the various degrees of freedom, or reaction coordinates. Since there are too many coordinates to depict individually, one or two coordinates, or combinations thereof, are usually selected that capture the essential behavior of the protein as it folds.
The overall shape of the energy landscape is that of a funnel. Recall that the configuration entropy , S(E), is a counting of the number of available states at a given energy, E. Mathematically, it is given by Ludwig Boltzmann’s (1844–1906) famous ca. 1872 expression, cast into its present form by Max Planck (1858–1947) around 1900, namely,
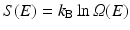
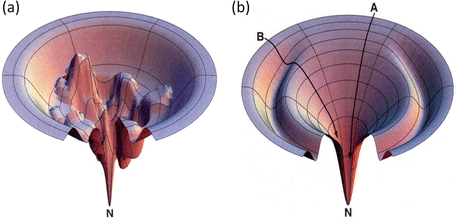
In this formula, Ω(E) denotes the number of microstates (conformations) of the protein. In its denatured state, a protein may be in any of a large number of possible configurations. This freedom rapidly vanishes as the protein folds into a low-energy form that is far more compact. As a result the energy landscape is funnel shaped, broad at the top, and narrow at the bottom near the native state. A pair of stereotypic funnel-shaped energy landscapes is shown in Fig. 3.3.
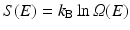
(3.1)

Fig. 3.3
Representative energy landscape s, or folding funnel s. Depicted at the right (b) is a fairly smooth folding funnel. Pathway A is typical of that taken by a fast, two-state folding protein while a protein taking pathway B encounters a ridge that must be surmounted and consequently slows its folding. The folding funnel shown in (a) differs from the other (b): its energy landscape is quite rugged. A protein taking a pathway to the native state (N) in this landscape will take orders of magnitude longer to reach its destination (from Dill Nat. Struct. Biol. 4: 10 © 1997 Reprinted by permission from Macmillan Publishers Ltd)
The folding process can be depicted as a trajectory connecting many points on the landscape, denoting the sequence of small conformational changes that the protein undergoes as it folds. As shown in the figure, a folding trajectory starts out at a denatured state located at the top of the landscape at a high potential energy and ends at the native state located at the bottom of the landscape at a low potential energy. The ability of protein to undergo a variety of motions, large and small, enables the protein to sample ensembles of states and substates at each point along its folding pathways generated by the macromolecular force s .
The amount of time required for a protein to fold into its native state is an important aspect of the process. This is referred to as a kinetic requirement. Not only must a protein fold into its native state, but also it must do so in a physiologically reasonable time interval. The speed depends critically on the topography of the potential energy surface. If the surface is studded with deep minima separated by tall hills, and the folding trajectories pass close to them, the rate of folding will be slow. In these situations, the protein will fall into the minima and must escape before proceeding with its step-by-step movements towards its native state. The deep minima are called kinetic trap s because of their slowing effects on the kinetics, or rates, of folding. Large and complex proteins, especially those involved in signaling pathways, tend to have rugged landscapes containing kinetic traps, or intermediate states, surrounded by high barriers. In contrast, small single-domain globular proteins often have landscapes that are fairly smooth. These proteins fold rapidly, lacking intermediate states and associated kinetic barriers that slow down the process. The difference between smooth and rough funnels is further highlighted in Fig. 3.4.
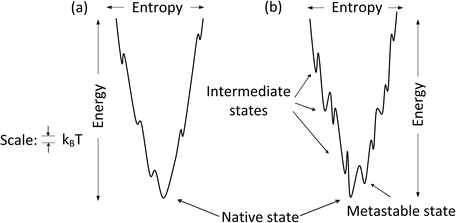

Fig. 3.4
One dimensional depiction of (a) smooth and (b) rugged folding funnel s
3.4 Metastable States
One of the features present in the rough funnel depicted in Fig. 3.4b is that of a low-lying intermediate states referred to as metastable states. Recall that one of the conditions for stability of the native state is that there be an appreciable energy gap between the native state and those lying above it. This condition is sometimes violated in a rough landscape. In these situations, a protein may dwell for a considerable amount of time in these low-energy states because of the high kinetic barriers. Although these are not states of minimal Gibbs free energy, proteins can still function in a useful fashion because of their long half-lives in those states.
In order to arrive at a state of minimal Gibbs free energy it must be kinetically accessible. In the case of many proteases, this condition has been exploited. These enzymes are synthesized as large proteins from which the active enzyme is subsequently cleaved. They typically contain a large amino-terminal proregion. This region is needed for kinetic accessibility and completion of the folding process to the native conformation. Once folding is complete and the protein is in its native state the proregion is removed. Removal of the proregion alters the energy landscape and the native state is no longer a state of minimal free energy. However, it is separated from the nearby lower-energy intermediate states by a high kinetic barrier and the enzyme is exceptionally stable. These kinetic situations are diagrammed in Fig. 3.5 for α-lytic protease.
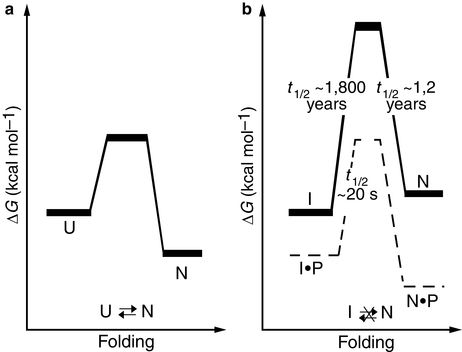

Fig. 3.5
Folding energetics (a) Thermodynamically controlled folding of a protein. U: unfolded state; N: native state. (b) Kinetic control of α-lytic protease folding and unfolding. The presence of the pro-region lowers the barrier for folding to the native state, and its absence raises the barrier thereby preventing its transition to one of several partially-unfolded intermediate states, I (from Jaswal Nature 415: 343 © 2002 Reprinted by permission from Macmillan Publishers Ltd)
Several examples of proteins that fold into functional metastable states rather than native states have been uncovered. Serpins (serine protease inhibitors) are a large family of protease inhibitors found in all kingdoms of life. These proteins regulate a variety of cellular processes; they help control complement cascades, angiogenesis, inflammation , tumor metastasis, apoptosis, axonal growth, and synaptic functions. Members of this large family include antithrombin which regulates blood coagulation, antitrypsin which mediates inflammation, PAI-1 which participates in tissue remodeling, and neuroserpin which regulates synaptic plasticity .
These proteins function as molecular mousetraps with an exposed reactive loop as the bait and the serine protease as the mouse. In its mousetrap-set form, the serpin resides in a metastable state. Binding of the serine protease to the reactive loop springs the trap and induces a major conformational enabling the serpin to transition to its native state.
3.5 Landscape Frustration and Spin Glasses
The energy landscape picture was introduced by Joseph Bryngelson and Peter Wolynes in a series of papers published in the late 1980s. The underlying inspiration for energy landscapes was provided in part by studies of spin glasses. Ordinary glasses are spatially disordered materials that lack the regularity of crystalline substances. These amorphous substances exhibit a “glass transition” from a solid and rather brittle form to a more liquid or molten state. Spin glasses are magnetic materials in which interactions between elements, rather than their positions, are disordered.
Mathematically, one can write an interaction term that closely resembles that of the Ising model, Eq. (2.6). To generate spin glass behavior the coupling factor J of the Ising model (discussed earlier in Chap. 2) is simply replaced by J ij which then assumes a random set of values, some positive and some negative:
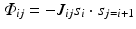
The result of this simple change can be dramatic. For many sets of coupling factors, spin orientations that produce good deep energy minima do not exist. Instead, the various constraints are in conflict with one another, and the energy landscape is fragmented into numerous shallow minima. Such systems are said to be “frustrated” because of the impossibility of simultaneously optimizing all the physical interactions and constraints with regard to the energy minimization.
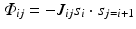
(3.2)
Proteins are in several respects just like spin glasses. They too exhibit frustration, unable to fold without encountering situations where there are no good energy lowering steps available. Instead, there are too many conditions to be satisfied simultaneously and consequently the local energy surface possesses numerous suboptimal minima. Referring back to Fig. 3.3a, the energy landscape being depicted is not smooth, but instead corrugated with numerous hills and valleys. Landscapes convoluted with large numbers of hills and narrow valleys are said to be rugged. The fast folding proteins discussed in Chap. 2 possess energy landscapes that are smooth allowing for the rapid folding under complete thermodynamic control. In contrast, proteins that encounter rugged landscapes fold orders of magnitude more slowly under kinetic control and may or may not reach a state of global minimum in the Gibbs free energy. One of the key concepts emerging from the studies of folding pathways is the principle of minimal frustration . This principle states that protein primary sequences have been evolutionarily selected to fold via pathways in energy landscapes that are as smooth as possible thereby encountering a minimal number of kinetic trap s.
Interestingly, hydrated protein motion s largely cease as the temperature is lowered below a critical point, referred to in the literature as the “glass-transition” temperature. Below that temperature range, approximately 200 K, the only protein motions remaining are vibrations and the protein is said to be in a glassy state. As the temperature is raised above the transition value the protein becomes more liquid-like; it can now undergo large-scale motions and, most importantly, it can carry out its designed functions, which had ceased along with the loss of its proper range of motions, its jiggling and wiggling, at the lower temperatures.
3.6 Motions Enable Proteins to Carry out Their Cellular Tasks
To recap, proteins jiggle and wiggle; they are flexible and dynamic, populate an ensemble of states, and continually undergo transition from one conformation to another over multiple timescales. They undergo motions ranging from rigid body rotations of entire subunits, to side-chain and backbone movements, to local folding and unfolding. These biophysical properties are central to protein function and evolution. They enable proteins to recognize and bind their multiple partners, and may well provide the means whereby enzymes accelerate the rates of chemical reactions and allosteric effectors alter the functional properties of proteins. In the case of binding and recognition, increases in dwell-time in a sparsely-populated excited state may enable that state to act as a doorway to oligomerization and fibril formation. As a result, a protein’s intrinsic flexibility can enable mutations and environmental factors to increase the likelihood that inappropriate aggregations occur and diseases emerge.
Protein recognition and binding: The classical model of ligand binding was introduced over a hundred years ago, in 1894, by the chemist Emil Fisher (1852–1919). Known as the lock-and-key mechanism of enzyme-substrate binding, the substrate (key) and enzyme (lock) are viewed as possessing complementary surfaces in terms of their shape and charge. These structures do not undergo major shape changes upon binding. Because their shapes fit into each other, the substrate is latched into the active site of the enzyme and this action initiates catalysis. To overcome shortcomings in Fisher’s lock-and-key mechanism, Daniel Koshland (1920–2007) presented an alternative picture of enzyme catalysis in 1958. In his induced-fit model, the substrate causes (induces) a substantial change in the three-dimensional conformation of the amino acids at the enzyme’s active site. These changes in shape, brought on by the substrate, properly align (uniquely fits) the catalytically active region of the enzyme with its substrate thereby enabling catalysis to take place.
The emergence of the protein folding landscape picture has led to an expanded view of how proteins bind one another. In the conformational selection model introduced in 1999, an ensemble of interconverting states exists prior to the interaction. When a protein comes into close proximity to its binding partner it forms an encounter complex that results in the selection (and stabilization) from the preexisting conformations those that best satisfy the geometric and electrostatic requirements for binding. These three mechanisms—static lock-and-key, semi-dynamic induced fit, and dynamic conformational selection—can operate either individually or in concert with one another to mediate protein recognition and binding.
Enzyme catalysis: Fast motions on a nanosecond timescale as well as slower motions spanning the microsecond to millisecond ranges underlie enzyme catalysis. That process has multiple steps. In addition to the chemical step, there are operations involving bringing together, aligning, opening and closing, and separating enzymes, substrates, cofactors , and products. Several steps in the reaction cycle are mediated by shifts in the equilibrium population of states in which a previously high-lying sparsely populated conformation becomes the new dominant low-lying state. If these shifts occur in a rate-limiting step they may explain the astonishing speedups observed in enzyme catalysis.
Allostery is dynamically driven: In an allosteric process , conformational perturbations at a particular site brought on by an effector generates functional changes at a distant, active site. Effectors are varied, ranging from ligands, to mutations and covalent modifications, to light and pH. The basic theory underlying “regulation (action) at a distance” was established 50 years ago in the mid-1960s by Monad, Wyman, and Changeux, formulated in terms of transitions between ‘tensed’ and ‘relaxed’ conformations, and by Koshland, Némethy, and Filmer based on their idea of an induced fit. The motivation for these studies was the desire to understand the sigmoidal (cooperative) binding of the multisubunit protein hemoglobin to molecular oxygen. This response property had been discovered in 1904 by Christian Bohr (1855–1911), father of Niels Bohr. Subsequent studies had provided details of the underlying hemoglobin physiology and Perutz and Kendrew had just produced a crystal structure upon which to anchor the theory. The resulting MWC and KNF models of allostery have been enormously influential and appear in all elementary textbooks on the subject.
In the intervening 50 years, the universe of proteins possessing allosteric properties has greatly expanded so that, today, allostery is regarded as a core biophysical property of most, if not all, dynamic (nonstructural), monomeric, as well as oligomeric, proteins. This expansion was made possible by (1) the development of solution NMR methods that enabled researchers to explore the dynamic processes underlying allosteric behavior and (2) by advances in theory, most notably the emergence of the energy landscape picture with protein motion s and ensembles of interconverting conformational states serving as key unifying concepts.
Effector events such as mutations or covalent modifications or ligand binding alter the internal motions of the protein. They change the fast internal dynamics of the protein as well as its slow internal motions. In addition, they cause sifts in the conformational equilibrium, that is, they generate a reordering of the free energies within the ensemble of ground and excited states. As a consequence some of the higher lying and less stable conformations have their energies lowered and become the new stable (ground) states. By this means, the changes propagate through the protein to the active site, selectively turning them on and off to potential interaction partners, thereby altering their functional properties.
Thermodynamically, the effectors produce changes in the protein’s configuration entropy and in its rotational and translational entropies. In more detail, the change in free energy of binding (ΔG bind) is the sum of the enthalpy of binding (ΔH bind) and the entropy of binding, which consists of contributions from the changes in protein, ligand, and solvent entropies:
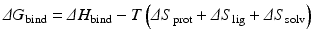
In general, entropic penalties engendered by binding are closely matched by gains in enthalpy. As a result small changes in conformational entropy can have large effects in determining binding affinities. The influence of changes in solvent entropy with regard to folding was discussed earlier. It also plays an important role in binding processes, and is typically thought of in terms of the hydrophobic effect . The change in the protein’s entropy consists of changes in its fast internal motions (its configuration entropy ) and in its rotational and translational entropies. The nature and magnitudes of these quantities has become a subject of great interest because of their emerging roles in disease causation and their potential exploitation in drug intervention.
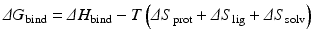
(3.3)
3.7 Experimental and Theoretical Methods of Exploring Protein Folding
Protein folding has been the subject of intensive studies for more than 60 years. During that time an ever-expanding suite of experimental and theoretical tools have been developed, starting with the previously discussed light microscopy, electron microscopy, and X-ray crystallography . These tools are often used synergistically with one another in order to explore the protein folding pathways and dynamic properties of the proteins as they fold and misfold. The most prominent of the theoretical/computational methods are
Molecular dynamics (MD)
Langevin/Brownian dynamics
Simulated annealing (SA)
Molecular dynamics had its beginnings in the 1950s with the advent of modern electronic computers. The first molecular dynamics calculations were carried out by Alder and Wainwright in 1957. These calculations were aimed at exploring liquid–solid phase transition s of atoms that were treated as simple hard spheres. In 1964, Rahman carried out an MD simulation of a realistic system of argon atoms. That study was followed in 1971 with an exploration by Rahman and Stilinger of liquid water that brought out the importance of water’s cooperative interactions and hydrogen-bonding network.
The first computer simulation of protein folding appeared in 1975 with the publication by Warshal and Levitt of their modeling and simulation study of the folding of bovine pancreatic trypsin inhibitor (BPTI), a small globular protein of known structure containing 58 amino acid residues. The first MD simulation study of BPTI dynamics was published shortly thereafter in 1977 by McCammon, Gelin, and Karplus. Their goal was to understand the dynamic fluctuations about the native conformation of the folded protein. Today, there are a number of widely used computer programs that enable users to carry out molecular dynamics simulations and protein structure prediction, dynamics, and design. These include CHARMM, AMBER, and GROMOS among others. Warshal, Levitt, and Karplus were awarded the 2013 Nobel Prize in Chemistry for their contributions to the field.
The folding of proteins is highly complex. As noted by Michael Levitt and Arieh Warshall in their 1975 paper, even a small protein of 50 residues has some 750 atoms and 200 degrees of freedom. When the solvent molecules are included the computational task becomes enormous. During the ensuing decades computer power has increased enormously and progressively more realistic and detailed simulations of protein folding have become possible, especially for the small globular proteins that fold rapidly.
Proteins fold through a sequence of states, most of which are transiently populated for a tiny fraction of a second. Partially folded intermediates are longer-lived for the reasons already discussed, and these can be studied to give valuable information on the routes taken by proteins as they fold and misfold. Three experimental methods—nuclear magnetic resonance (NMR), hydrogen-deuterium exchange , and ϕ-value analysis are especially well suited for exploration of intermediate states and protein dynamics. These methods will be described following an examination of the theoretical, computational tools.
3.8 Molecular Mechanics (MM)
In molecular mechanics treatments of protein folding, the macromolecular force s between atoms are modeled in an empirical fashion. Two classes of forces are considered—covalent and noncovalent. Covalent bonds, in which electrons are shared, are the strongest of the bonds. They form the strong peptide linkages comprising the protein backbone. These bonds are thought of as operating in an elastic spring-like manner. In elastic springs, there is an equilibrium point and departures from that point due to stretching or compression build up potential energy. Once the perturbing force is removed the system returns to its equilibrium point.
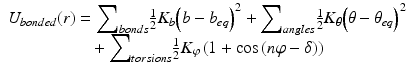
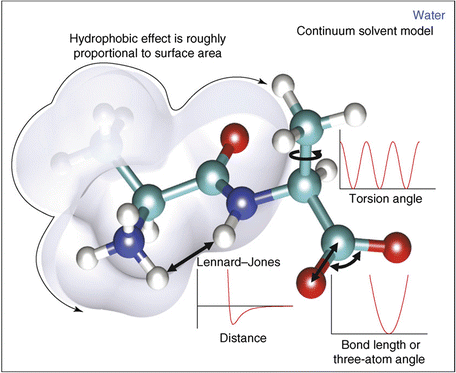
In molecular mechanics , three covalent force terms are defined. These describe the possible stretching, bending, and torsional (dihedral) motions about the bond axis. These three terms are given by Eq. (3.4), and are illustrated in Fig. 3.6. The length (bonds) and angles terms take the form of a harmonic potential that follows from Hooke’s (in which the elastic spring force F is the product of the spring constant and the displacement from the equilibrium point). It has a minimum at the equilibrium position while the torsions term is a periodic function of the torsion angle.
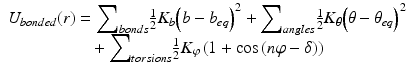
(3.4)

Fig. 3.6
Potential energy functions including the hydrophobic effect (from Boas Curr. Opin. Struct. Biol. 17: 199 © 2007 Reprinted by permission from Elsevier)
The noncovalent forces include various combinations of point charge and dipole forces. These terms are jointly modeled as the sum of a Lennard-Jones, 6–12 potential, and a Coulomb-like point charge term as given by Eq. (3.5). These terms are summed over all atoms in the protein. The term in the Lennard-Jones (L-J) potential that varies as the sixth power of the radius is an attractive one while the other contribution, from the term varying as the twelfth power, is repulsive. The overall shape of the potential is depicted in Fig. 3.6. As can be seen in that figure the net effect being captured is strong repulsion at short distances corresponding to interpenetration of the electron clouds forbidden by the Pauli Exclusion Principle. There is a distance where the two terms just cancel one another. That distance is referred to as the van der Waals radius, and there is a minimum in the potential at the equilibrium radius.
![$$ {U}_{\mathrm{non}-\mathrm{bonded}}\left({r}_{ij}\right)={\displaystyle \sum}_{i<j}\left\{\left[\frac{a_{ij}}{r_{ij}^{12}}-\frac{b_{ij}}{r_{ij}^6}\right]+\frac{q_i{q}_j}{r_{ij}}\right\} $$](/wp-content/uploads/2016/09/A311304_1_En_3_Chapter_Equ5.gif)
Because of their importance, hydrogen bonding and hydrophobic effect s require additional attention. The hydrogen bonds in this model are handled in an approximate fashion by suitably adjusting the constants in the L-J and Coulomb potentials. In some implementations, an additional term similar to that presented in Eq. (3.5) is appended. This term is often taken to be of an angle-dependent 12-10 form rather than the standard, angle-independent 12-6 form. The angle in this term represents the donor-hydrogen-acceptor angle.
![$$ {U}_{\mathrm{non}-\mathrm{bonded}}\left({r}_{ij}\right)={\displaystyle \sum}_{i<j}\left\{\left[\frac{a_{ij}}{r_{ij}^{12}}-\frac{b_{ij}}{r_{ij}^6}\right]+\frac{q_i{q}_j}{r_{ij}}\right\} $$](/wp-content/uploads/2016/09/A311304_1_En_3_Chapter_Equ5.gif)
(3.5)
Hydrophobic interactions can be handled in one of two ways. In explicit solvation models, solvation energies are added that describe solvent-solvent and solvent-protein interactions. In the simpler continuum approaches, hydrophobic interactions are described in terms of the solvent accessible surface area (SASA) (Fig. 3.6). This quantity was first introduced by Lee and Richards in 1971 in their study of packing densities. Both approaches enable a more accurate treatment of the interactions with the water outside the protein and with water contained within the interior cavities being formed.
3.9 Molecular Dynamics (MD)
Molecular dynamics is the name given to a suite of computer simulation methods for studying how large systems of interacting atoms and molecules evolve over time. In this approach, Newton’s equations of motion are numerically integrated using the potential functions from molecular mechanics to compute the forces. Introducing standard “dot notation” Newton’s laws of motion are
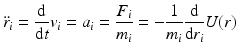
with
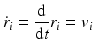
In Eq. (3.6), the potential energy, U(r), is the sum of the bonded and nonbonded potentials given by Eqs. (3.4) and (3.5), plus any additional terms that describe hydrogen-bonding contributions and hydrophobic effect s. Once the potentials are specified the equations of motion are integrated. Numerical techniques known as finite-difference methods are used to convert the equations of motion into a form suitable for integration on a computer. The basic idea is to take the positions and momentum of each particle at a given time and compute how each quantity changes over a small time interval. One of the most widely used time stepping methods is the Verlet algorithm. The relevant expression is derived by first doing a Taylor’s series expansion of the positions at time t + Δt where Δt is the time step size, and keep only the first few terms:
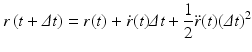
Upon carrying out some algebraic manipulations the Verlet algorithm can be produced:
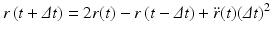
In deriving this expression the velocities have been eliminated. The positions at time t + Δt are computed from the positions at times t and the previous time t − Δt and from the forces at time t through the acceleration term. In some cases, the velocities are important. In those situations another time stepping expression known as the velocity Verlet algorithm is used. It takes the form:
![$$ \dot{r}\left(t+\varDelta t\right)=\dot{r}(t)+\frac{1}{2}\left[\ddot{r}(t)+\ddot{r}\left(t+\varDelta t\right)\right]\varDelta t $$](/wp-content/uploads/2016/09/A311304_1_En_3_Chapter_Equ10.gif)
The step size, Δt, is a critical quantity. It is customary to use femtosecond (10−15 s) time steps in order to account for the fast motions—the atomic fluctuations, and side-chain and loop motions. However, even the most-rapidly folding motifs, supersecondary structures, and domains require microseconds (10−6) to milliseconds (10−3 s) to fold. Thus, one has to integrate the equations of motion over 1012 time steps. Furthermore, the number of conformational states is enormous since there are perhaps tens of thousands of atoms present (especially when taking into account the attendant water molecules).
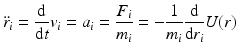
(3.6)
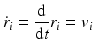
(3.7)
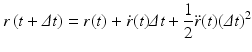
(3.8)
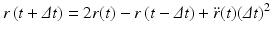
(3.9)
![$$ \dot{r}\left(t+\varDelta t\right)=\dot{r}(t)+\frac{1}{2}\left[\ddot{r}(t)+\ddot{r}\left(t+\varDelta t\right)\right]\varDelta t $$](/wp-content/uploads/2016/09/A311304_1_En_3_Chapter_Equ10.gif)
(3.10))
One of the ways to meet the computational challenge is to simplify the energy landscape by introducing a small number, one or two, of order parameters or effective coordinates. The most widely used of these is the order parameter usually designated by the symbol “Q” that represents the number of tertiary native contacts in a given conformation of the protein under study. If two residues are close to one another in space, that is, their α-carbons are within ~7 Å of one another, they are said to be in contact. If these contacts are found in the native state, then they are said to be a native contact and the order parameter Q counts the number of these, that is, it is a measure of nativeness. The unfolded state has few native contacts while in the native state Q is maximal. This type of order parameter is intended to capture the most salient features of the underlying energy landscape, that is, the prominent valleys, ridges, and basins encountered by the protein as its folds into its native state.
Shown in Fig. 3.7 is an energy landscape for hen lysozyme, a protein consisting of 129 amino acid residues organized into two domains, α and β. This protein can fold along two distinct pathways, one rapid and the other slow in which there is a prominent kinetically trapped folding intermediate. The figure combines theoretical simulations with experimental data acquired by means of nuclear magnetic resonance and hydrogen-deuterium exchange , and utilizes a pair of order parameters to simplify the landscape.
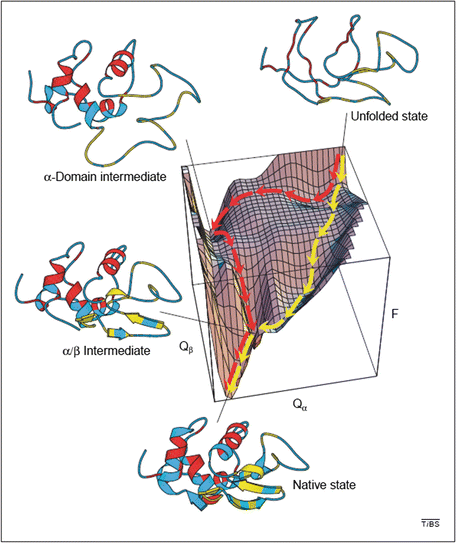

Fig. 3.7




Energy landscape describing the folding of hen lysozyme. Plotted along the vertical axis is the free energy while the horizontal axes represent the number of native contacts. The yellow trajectory represents the fast pathway in which the α and β domains form concurrently and only transiently populate the α/β intermediate state. The red trajectory passes through a long-lived intermediate state is which only the α domain has formed its secondary structure. The system must then pass over a high energy barrier and may partially unfold in order to complete its passage to the native state (from Dinner et al Trends Biochem. Sci. 25: 331 © 2000 Reprinted by permission from Elsevier)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








