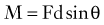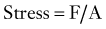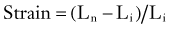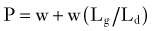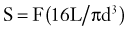CHAPTER 291 Basic Principles of Spinal Internal Fixation

Steven D. Chang, Neil R. Crawford, Volker K.H. Sonntag, Curtis A. Dickman

In the spine there are 28 vertebrae: 7 cervical vertebrae, 12 thoracic vertebrae, 5 lumbar vertebrae, and 4 sacral vertebrae that typically exist as a single fused unit. From cranial to caudal, as the biomechanical demands and functions change, the size of the vertebra increases and the orientation of the facets gradually changes from parallel sloping to upright blocking. The normal spine is balanced sagittally with a cervical lordosis, a thoracic kyphosis, and a lumbar lordosis.

Passive spinal stability is provided by the facet joints, intervertebral disks, and numerous ligaments. Because of the many stabilizing structures, identifying the level of instability beyond which the passive stability requires internal fixation is challenging. Several authors have proposed systems for grading instability, but perhaps the best known is Denis’ three-column theory,¹ devised after retrospectively reviewing the radiographic images of 412 thoracolumbar fractures. According to this theory, the anterior column consists of the anterior half of the vertebral body, the anterior half of the annulus fibrosis, and the anterior longitudinal ligament. The middle column consists of the dorsal half of the vertebral body, the dorsal half of the annulus fibrosis, and the posterior longitudinal ligament. The posterior column consists of the pedicles, facets, lamina, pars interarticularis, and posterior ligamentous complex. Denis proposed that an injury that compromises two of the three columns leads to pathologic instability at the affected level (Fig. 291-1).

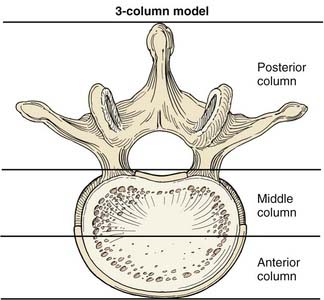
FIGURE 291-1 Illustration of a vertebral body showing the columns of spinal stability as originally described by Denis.¹

(Used with permission from Barrow Neurological Institute, Phoenix, AZ.)

The spinal motion segment—two adjacent vertebrae and their interconnecting tissues—is the fundamental unit of study on which biomechanical principles of internal fixation are based. Abnormal movement or instability of a motion segment can lead to clinical symptoms of myelopathy when the spinal cord is compromised, to radicular symptoms when the nerve root foramen or cauda equina is compromised, and to back pain when abnormal motion occurs.

The traditional goal of surgical treatment is to correct pathologic instability by promoting bony fusion at the affected level. To ensure good fusion, orthotic immobilization has been the standard of care for decades; however, mechanical hardware as an alternative adjunct to fusion has become more popular because it allows early mobilization of the patient. More recent techniques avoid fusion altogether and attempt to restore stability by dynamic internal fixation, relying on implanted hardware to bear loads previously borne by disks, facets, and ligaments.

The goal of spinal internal fixation for fusion is to reconstruct the compromised columns within a spinal motion segment with nonbiologic materials to afford temporary immobilization and stabilization until bony fusion can develop. Fixation is successful when a construct can withstand the wear and tear of mechanical stresses and strains until fusion occurs.

The goal of dynamic spinal internal fixation is to reconstruct the compromised columns with nonbiologic materials to create new permanent limiters to motion that maintain spinal motion within normal stable ranges. Such fixation is successful when a construct can withstand the wear and tear of mechanical stresses and strains for the rest of a patient’s life.

For both rigid and dynamic fixation systems, successful application of the available hardware and instrumentation techniques begins with a sound and fundamental understanding of the origin of these stresses and strains and how they are modified by different instrumentation techniques.

Basic Biomechanics

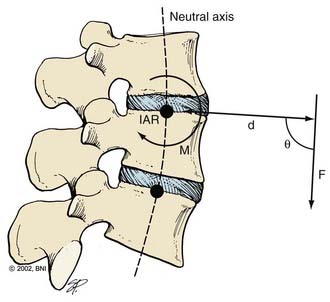
The spine is subjected to numerous forces, typically from gravitational loads, muscular and ligamentous loads, and acceleration and deceleration loads. Forces applied to the spine can be envisioned as vectors (Fig. 291-2). Force vectors applied to the spine can be directed to induce compression, tension, shear, bending, or torsion. A force vector has magnitude and direction in three-dimensional space. Force causes displacement or distortion of an object if it is, respectively, unopposed or opposed.

FIGURE 291-2 Lateral illustration of a spinal motion segment showing the instantaneous axis of rotation (IAR) and the neutral axis of the spinal column (dashed line) during flexion. A force vector (F) is depicted applied at an angle (θ) and distance (d) relative to the IAR. The moment (M) occurring at the IAR is depicted by the curved arrow. The magnitude of the moment is represented by the equation M = Fdsinθ.

(Used with permission from Barrow Neurological Institute, Phoenix, AZ.)

The effect of a force depends on its orientation to a body’s axis of rotation or neutral axis. The axis of rotation is the axis about which a structure bends or rotates. For example, when a door swings open, a line through its hinges would be the axis of rotation. During movement of the spine, the axis of rotation shifts through a range of positions, unlike the fixed axis of rotation of a hinged door. Instantaneous measurement at one time point provides one “snapshot” of the location of the axis of rotation during a particular phase of the movement, or an instantaneous axis of rotation (IAR). In the normal spine, the IAR for a given bending or twisting motion usually remains in or near the disk space because the flexible disk material deforms more easily than the rigid vertebral bodies. The location of the IAR can often be predicted from the curvature of the facet joints and disk.²

The neutral axis is the longitudinal axis along which no axial stresses or strains occur during bending or twisting. For example, when the lumbar spine bends in flexion, the anterior disk fibers compress axially while the posterior fibers stretch axially. The fibers in between, through which the neutral axis runs, neither compress nor stretch (although they may shear anteroposteriorly if the axis of rotation is below the disk space, as is often the case). The neutral axis intersects the IARs of each spinal motion segment along the entire spine at right angles (Fig. 291-2). The neutral axis is a term that applies only to bending or twisting of the spine. No neutral axis exists during pure distraction, compression, or shear because the entire spine is under unidirectional loading in these cases.

Forces applied to the spine are often interpreted in terms of the moments they create at locations of interest, such as at the axis of rotation, along the neutral axis, or at the site of fixation. The moment, M, created by a force, F, is described by the formula

where d is any measured distance between the line of action of the force and the location where the moment is assessed, and θ is the angle between the line along which distance is measured and the force vector. The magnitude of the moment increases as the distance from the line of force to the location where moment is measured (i.e., the moment arm) increases.

Newton’s third law states that each force is opposed by an equal and opposite force. When an internal force from the muscles or an external force from gravity, acceleration, or contact is applied to the spinal motion segment, the ligaments, disk, and joint surfaces react as the primary sources of this equal and opposing force. The mechanical properties of these supporting tissues dictate how the force is to be dissipated by the system.

When normalized, the loads and displacements that occur within a system are defined as stress and strain. Stress is defined as the force, F, applied over an initial cross-sectional area, A.

Strain is defined as the change in length of a material over the original length of the material, as defined in the formula

where L_n is the new length and L_i is the initial length. Stress and strain are directly proportional to each other; as stress increases, strain increases. The amount of stress needed to produce a given strain (i.e., the ratio of stress over strain) is Young’s modulus, or the stiffness of a material.

Most biologic materials are much less stiff than the materials used in spinal fixation (Table 291-1). The modulus of elasticity of a material describes the stress (force per unit of cross-sectional area) per unit of strain (linear deformation per unit of length) in the elastic region. A higher modulus of elasticity implies a stiffer, or more rigid, implant. However, most biologic materials have both viscous and elastic (viscoelastic) properties, whereas implant materials act primarily as elastic elements. The viscous properties present in the spine permit long-term and rate-dependent responses to loads. With the application of stress to a material with viscoelastic properties, elastic strain is apparent immediately, whereas viscous strain becomes apparent over time as the stress in the system declines exponentially. Strains applied to viscoelastic materials at a high rate, such as during a car accident, cause higher stresses in the tissues resisting the strains than the same strains applied at a lower rate, such as during a lifting accident.

TABLE 291-1 Material Properties of Bone and Biomaterials

MATERIAL	YIELD STRENGTH (MPa)	MODULUS OF ELASTICITY (MPa)
Bone
Cancellous bone	2	90
Lumbar vertebra	5	160
Cervical vertebra	10	230
Cortical bone	150	12,000
Biomaterials
Polyethylene (UHMWPE)	20	870
Polymethylmethacrylate	100	2,400
Polyetheretherketone (PEEK)	140	3,400
Ti (Grade 4)	560	104,000
Ti6Al4V	825	114,000
Stainless steel (316)	205	193,000
Cobalt chromium	620	233,000

UHMWPE, ultra-high-molecular-weight polyethylene.

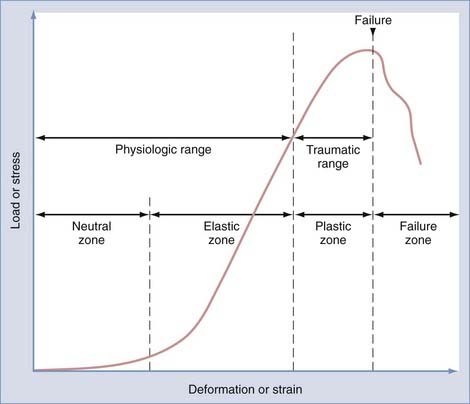
Physiologic range of motion is the range through which the spine can move without injury and is dictated by the viscoelastic properties of the spinal motion segment (Fig. 291-3). For small deformations, ligaments and other soft tissues are lax; consequently, the stiffness of the system is low. The portion of the range of motion at which little stress is required to produce large deformations of the spinal motion segment is known as the neutral zone. In contrast, in the elastic zone, exceedingly larger forces are required to produce small incremental changes in deformation. In the elastic zone, the ligaments and other soft tissues are stretching, whereas in the neutral zone, they have not yet begun to stretch.³

FIGURE 291-3 Graph illustrating range of motion (ROM) and other parameters in a spinal motion segment as they relate to stress and strain. The neutral zone is the range of spinal movement in which large deformations occur in response to small amounts of applied stress. The elastic zone is the range in which exceedingly larger forces are required to produce small incremental changes in the ROM. The physiologic range is the ROM and includes both the neutral and elastic zones. Once the elastic zone is exceeded, the system sustains injury, which can lead to further deformation and eventual failure of the spinal motion segment.

(Adapted from White AA, Panjabi MM. Clinical Biomechanics of the Spine, 2nd ed. Philadelphia: Lippincott Williams & Wilkins; 1990:21.)

When the elastic zone and range of motion are exceeded, the elastic limits of the tissues are surpassed and permanent (plastic) deformation occurs. In a biologic system, the source of plastic deformation is tearing of individual tissue fibers. In a nonbiologic system, the source of plastic deformation is the sliding of atoms past one another into a new lattice location, or microfractures of the material’s structure. In both systems, larger scale tears and fractures represent failure of the system.

Different materials, biologic and nonbiologic, display different behaviors when they reach the traumatic and failure zones. Some materials fail gradually, and others fail instantaneously. Materials such as methylmethacrylate (bone cement), ceramic, and some alloys may be strong, but they are brittle and fail completely with small deformations. Other materials are better at tolerating strain. Steel, for example, gradually bends instead of snapping when its elastic limits are exceeded. When designing or choosing a construct for stabilizing a spinal motion segment, a key consideration is whether the stresses and strains that the hardware must endure before failing exceed the stresses that patients will generate in their lifetime at the site of the hardware (after accounting for load sharing between bone and hardware).

When a normal spinal motion segment fails, the elastic limit of the ligaments, disk, or bone is exceeded. When a spinal fusion construct fails, the elastic limit of either the fixation hardware or the remaining biologic tissues is exceeded. In either fused or normal motion segments, stability is afforded when the elastic limits of the tissues or mechanical hardware are obeyed. Failure of the system leads to the dissipation of the unopposed force or moment applied to the system. Translation of this load to the neural elements of the spine can result in mechanical compression or injury of the spinal cord.

Physiologic Spinal Loading

When the normal spine assumes a physiologic upright position, the center of gravity may be far anterior to the spine’s IAR and neutral axis. The anterior location of the body’s center of gravity imposes a flexion bending moment on the spine, which is counteracted by extensor muscle forces in the dorsal elements of the spine posterior to the IAR. The total compressive load, P, caused by body weight plus muscle contraction to counteract the bending moment imposed by gravity in a spinal motion segment is estimated as

where w is the weight of the body above the spinal motion segment, L_g is the distance from the IAR to the center of gravity, and L_d is the distance from the IAR to the dorsal muscles of the spine. Because L_g is always larger than L_d when standing upright, the actual compression experienced by the spinal motion segment is often two to four times that due to simple gravitational loading. When the orientation of the IAR or center of gravity changes, the load that must be exerted by the posterior muscles changes. When holding an object in one’s arms in front of the torso, for example, the center of gravity is displaced anteriorly from the IAR, and the compressive load increases. This point is important because when the posterior muscle tissues are compromised by surgery or trauma—or when the IAR is shifted by surgery, degeneration, or trauma—spinal biomechanics change significantly. Another observation from this analysis is that an obese patient, whose center of gravity is shifted farther anterior, will have more difficulty coping with compromised dorsal musculature than a fit patient.

Basics of Spinal Instrumentation

Historical anecdotes cite the use of screws, rods, and wires to correct and stabilize spinal deformities as early as the mid- to late 1800s. However, the rapid advances that have led to contemporary spinal instrumentation and fixation techniques began in 1962, when Harrington introduced his spinal instrumentation system. To appreciate the intrinsic shortcomings and strengths of different fixation techniques, one must be familiar with the mechanical and metallurgic qualities of the components in any given instrumentation system.

Screws

Screws are used in a variety of applications in the spine. Each application requires different biomechanical considerations. Regardless of the specific application, all screws share common features. Each screw has a head, a shaft, and a threaded portion. The minor diameter of the screw is the width of the shaft beneath the threads; the major diameter is the width of the shaft with the threads.

The mechanical bending strength of a screw is a function of the diameter of the shaft. Changes in the minor diameter significantly increase or decrease the bending strength of a screw.⁴ A twofold change in the minor diameter increases the screw’s bending strength eightfold because the highest stress, S, applied to a screw during three-point bending is a function of the equation

where F is the force applied at either end of the screw, L is the length of the screw, and d is its minor diameter. Often, the bending moment or shear force at the proximal aspect of the screw shaft is large because of the orientation of forces at the screw head-plate junction, which can mimic the claw of a hammer prying the head of a nail. Because the transition from the threaded to the nonthreaded portion of the shaft is accompanied by an abrupt increase in the minor diameter of the screw, this area can function as the weak point in the screw and is often the site of screw failure.^5,⁶

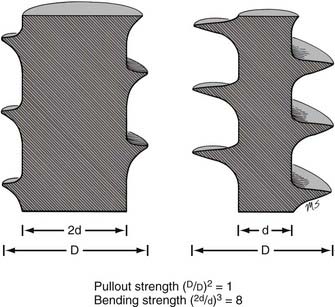
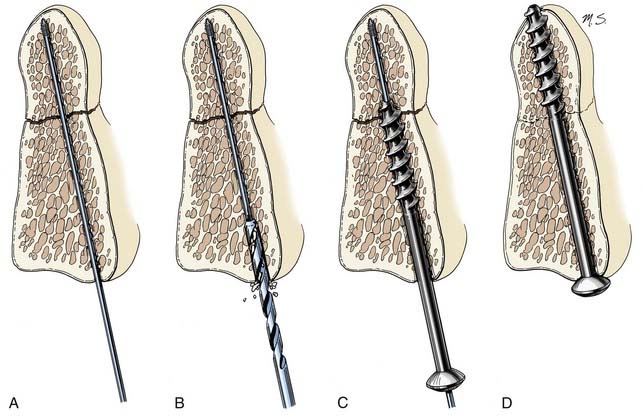
The pullout strength of a screw depends on numerous variables. Most important are the screw-bone interface and the quality of the bone.⁴ Cortical bone provides a more secure purchase than does trabecular bone. Diseased osteopenic bone provides poor structural support. During screw insertion, trauma related to poor drilling techniques or overheating can impair the screw’s purchase or lead to the pathologic resorption of bone around the screw.⁷ Rescue screws used in cervical plating systems and thoracolumbar pedicle screws have a wider diameter to recover purchase in a stripped or enlarged screw hole. The pullout strength of a screw depends on the depth at which the screw is placed and the screw’s major diameter.⁸ Note that unlike a screw’s bending strength, the pullout strength is affected little by the screw’s minor diameter (except when the dimensions of the major and minor diameters are too close to create bite, or when the bone surrounding the hole is nonuniform). Hence, a twofold increase in minor diameter that causes an eightfold increase in bending strength should have little or no effect on pullout strength (Fig. 291-4).

FIGURE 291-4 The theoretical bending strength of a screw is directly proportional to the third power of the minor screw diameter (d). The pullout strength of a screw is proportional to the square of the major diameter (D) and is affected by the density of the bone beneath the screw threads. Theoretically, a twofold increase in the minor screw diameter with no change in the major diameter increases the bending strength eightfold without affecting the pullout strength.

(Used with permission from Barrow Neurological Institute, Phoenix, AZ.)

Lag screws place bone fragments under compression (Fig. 291-5). The shaft of a lag screw has both threaded and nonthreaded portions. The threaded portion of the shaft, which is the distal portion, is used to engage a distal bone fragment. As the screw is tightened, the distal fragment is compressed toward the proximal fragment as long as the threaded portion of the shaft does not cross the fracture line. A lag effect in a fully threaded screw also can be obtained by drilling the proximal portion of the screw hole to the screw’s major diameter so that the screw obtains no purchase proximally. A lag effect can also be obtained by using a screw with a threaded shaft divided into two portions based on a difference in the pitch and depth of the thread. This difference causes the distal portion of the screw to advance more rapidly than the proximal portion, which consequently compresses the bone fragments.

FIGURE 291-5 Techniques of cannulated screw insertion for fixation of an odontoid fracture. A, A threaded K wire is inserted into the dens. Hollow tools and screws are subsequently threaded over the K wire into the bone. B, A 5-mm deep pilot hole is drilled in the body of the dens under fluoroscopic visualization. The proximal hole allows the screw threads to purchase the bone. C, A self-tapping, partially threaded lag screw is placed over the K wire. The screw threads should engage only the distal bone fragment. D, The tip of the screw should barely penetrate the tip of the dens. The K wire is removed.

(Used with permission from Barrow Neurological Institute, Phoenix, AZ.)

Cannulated screws have a hollow shaft that allows the screw to be placed over a thin surgical guidewire. These screws are used when precise placement is needed, as in transarticular screw placement. The hollow aspect of the screw’s shaft slightly reduces its bending strength but does not affect its pullout strength.⁹ Because the outer region of metal in a screw shaft is more important in resisting bending than the core, substantial bending strength can still be maintained with cannulation. For example, a 2.5-mm minor diameter screw with a 1.5-mm diameter cannula is theoretically 87% as strong in bending as a solid 2.5-mm diameter screw; a 3-mm minor diameter screw with a 1.5-mm diameter cannula is theoretically 94% as strong in bending as its solid counterpart.

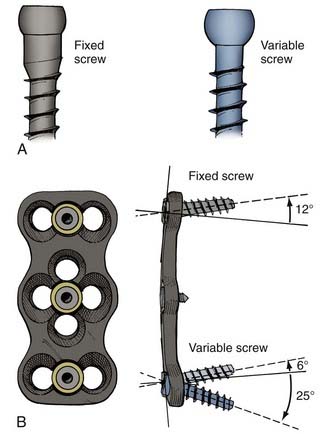
Screws also differ based on their relationship to the overlying plate or rod (Fig. 291-6). When the screw head’s interface with the overlying apparatus is rigid, the system is described as constrained. When the screw head’s interface is nonrigid, the system is described as nonconstrained. The design of the hardware determines whether a constrained screw can have a variable trajectory during placement. For example, in most cervical plating systems, screws placed with a fixed trajectory are, by definition, constrained screws because of how the screw head–plate interface is designed. In contrast, in most pedicle screw systems, the trajectory of the screw does not affect the screw’s ability to rigidly fixate to the overlying rod, so these screws can be described as variable-trajectory screws in a constrained system.

FIGURE 291-6 A, Fixed- and variable-trajectory screws differ, based on their interface with the overlying implant. Shown are the screws in the Atlantis cervical plating system (Medtronic Spinal & Biologics, Memphis, TN). The fixed screw head is shaped so that it locks at its interface with the overlying plate to prevent toggling. The variable screw is shaped so that it can toggle. B, Fixed-trajectory screws function like a fixed moment arm cantilever beam fixation device. This rigid fixation device provides optimal biomechanical stability. It is preferred when fixation is needed to correct instability caused by trauma. In contrast, variable-trajectory screws function like a tension band or nonfixed moment arm cantilever because the angle of fixation has the ability to change as depicted. This feature may allow the implant to dissipate the stress and strain introduced as a graft subsides over time.

(Used with permission from Barrow Neurological Institute, Phoenix, AZ.)

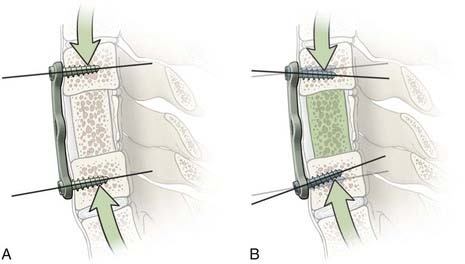
Constrained screws provide more rigid immobilization and are generally more desirable when treating traumatic instability. Nonconstrained screws are desirable when treating degenerative instability because they allow settling at the screw-plate interface while the adjacent fusion mass subsides over time. Nonconstrained constructs have helped solve the problem of stress shielding of the bone graft and thus have led to increased fusion rates in patients with degenerative conditions.¹⁰ Although materials used for spinal fixation are usually stiffer than any of the surrounding biologic materials, some of the more recent fixation devices use materials with mechanical properties better matching the stiffness of bone, such as PEEK (polyetheretherketone; see Table 291-1). Such material selection mitigates stress shielding, a phenomenon in which the majority of the natural loading of the spine is borne by the hardware instead of the bone. Wolff’s Law states that bone will adapt to the loads under which it is placed. Therefore, if the hardware bears the majority of the load, the adjacent bone will atrophy and disappear, possibly leading to an unstable nonunion. A more favorable situation is where the fusion hardware and bone graft for fusion participate in load sharing, in which Wolff’s Law leads to formation of new bone across the graft and diminishing loads across the hardware over time (Fig. 291-7).