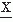EEG Analysis: Theory and Practice
Fernando H. Lopes Da Silva
Analysis of electroencephalography (EEG) signals always involves questions of quantification; such questions may concern the precise value of the dominant frequency and the similarity between two signals recorded from symmetric derivations at the same time or different times. In these examples, there is a question that can be solved only by taking measures with regard to the EEG signal. Without such measures, EEG appraisal remains subjective and can hardly lead to logical systematization. Classic EEG evaluation has always involved measuring frequency and/or amplitude with the help of simple rulers. The limitations of such simple methods are severe, particularly when large amounts of EEG data must be evaluated and the need for data reduction is felt strongly, as well as when rather sophisticated questions are being asked, such as whether EEG signal changes occur in relation to internal or external factors, and how synchronous are EEG phenomena occurring in different derivations.
Clear replies to these questions require some form of EEG analysis. However, such analysis not only is a problem of quantification, but also involves elements of pattern recognition. Every electroencephalographer knows that it is sometimes extremely difficult to cite exact measures for such EEG phenomena as spikes, sharp waves, or other abnormal patterns; the experienced specialist is able to detect them only by “eyeballing.” These types of problems may be solved using pattern recognition analysis techniques, based on the principle that features characteristic of the EEG phenomena have to be measured. This phase of feature extraction is followed by classification of the phenomena into different groups. EEG analysis thus implies not only simple quantification, but also feature extraction and classification.
The primary aim of EEG analysis is to support electroencephalographers’ evaluations with objective data in numerical or graphic form. EEG analysis, however, can go further, actually extending electroencephalographers’ capabilities by giving them new tools with which they can perform such difficult tasks as quantitative analysis of long-duration EEG in epileptic patients and sleep and psychopharmacologic studies.
The choice of analytic method should be determined mainly by the goal of the application, although budget limitations must also be taken into consideration. The development of an appropriate strategy rests on such practical facts as whether analysis results must be available in real time and online or may be presented offline. In the past, the former requirement would pose considerable problems, solvable only by adopting a rather simple form of analysis; the development of new computer technology has provided more acceptable solutions. Another practical consideration is the number of derivations to be analyzed and whether the corresponding topographic relations have to be determined or the analysis of one or two derivations is enough; the latter may suffice during anesthesia monitoring or in sleep research. Whether the analysis of a relatively short EEG epoch is sufficient or must involve very long records, for instance, up to 24 hours is another important factor.
In short, the method of analysis must be suited to the purpose of the analysis. Among the different purposes are the following: (i) determining whether a relatively short EEG record taken in a routine laboratory is normal or abnormal; (ii) classifying an EEG as abnormal, for example, as epileptiform or hypofunctional; (iii) evaluating changes occurring in serial EEG; and (iv) evaluating trends during many hours of EEG monitoring, such as under intensive care conditions for heart surgery or in long-term recordings in epileptic patients.
GENERAL CHARACTERISTICS
The EEG is a complex signal, the statistical properties of which depend on both time and space. Regarding the temporal characteristics, it is essential to note that EEG signals are everchanging. However, they can be analytically subdivided into representative epochs (i.e., with more or less constant statistical properties).
Estimates of the length of such epochs vary considerably because of dependence on the subject’s behavioral state. When the latter is kept almost constant, Isaksson and Wennberg (1) found that, over relatively short-time intervals, epochs can be defined that can be considered representative of the subject’s state; in this study, some 90% of the EEG signals investigated had time-invariant properties after 20 seconds, whereas less than 75% remained time invariable after 60 seconds. Empirical observations indicate that EEG records obtained under equivalent behavioral conditions show highly stable characteristics; for example, Dumermuth et al. (2) showed that variations in mean peak (beta activity) of only 0.8 Hz were obtained in a series of 11 EEGs over 29 weeks. In this respect it is interesting to consider the studies of Jansen (3) and Grosveld et al. (4); these authors investigated the possibility of correctly assigning EEG epochs (duration 10.24 seconds) to the corresponding subject by means of multivariate analysis, using half of the EEG epochs recorded from 16 subjects as a training set for the classification algorithm. Using 4 to 10 EEG features, it was found that in 80% to 90% of the cases of EEG epochs were assigned correctly to the corresponding subject. McEwen and Anderson (5) introduced the concept of wide-sense stationarity in EEG analysis; they
proposed a procedure for determining whether a set of signal samples (e.g., an EEG signal) can be considered to belong to a wide-sense stationarity process. Their procedure consisted of calculating the amplitude distributions and power spectra of sample subsets and showing that they do not differ significantly using the Kolmogorov-Smirnov statistic. From this study it was concluded that, for EEG epochs (awake condition or during anesthesia) of less than 32 seconds, the assumption of wide-sense stationarity was valid more than 50% of the time.
proposed a procedure for determining whether a set of signal samples (e.g., an EEG signal) can be considered to belong to a wide-sense stationarity process. Their procedure consisted of calculating the amplitude distributions and power spectra of sample subsets and showing that they do not differ significantly using the Kolmogorov-Smirnov statistic. From this study it was concluded that, for EEG epochs (awake condition or during anesthesia) of less than 32 seconds, the assumption of wide-sense stationarity was valid more than 50% of the time.
On the basis of this type of empirical observation, it can be assumed that relatively short EEG epochs (˜10 seconds) recorded under constant behavioral conditions are quasi-stationary. Elul (6) remarked that the EEG is related to intermittent changes in the synchrony of cortical neurons; thus, he characterized the EEG as a series of short epochs rather than a continuous process.
The fact that EEG signals have different characteristics depending on the place over the head where they are recorded is essential to all EEG recordings. Therefore, in any method of EEG analysis, topographic characteristics have to be taken into account. This means that one should choose EEG montages carefully, in view of the objectives of the analysis. The topographic aspects appear most clearly in the simple case of comparing EEG records from symmetric derivations; indeed, the use of the subject as his or her own control through right-left comparisons is a cornerstone of the neurologic examination. Therefore, right-left comparisons are also paramount in any practical clinical system of EEG analysis.
BASIC STATISTICAL PROPERTIES
Some of the underlying assumptions of the most common methods of EEG analysis will be discussed briefly. Gasser (7) has provided a more fundamental discussion of this topic; here, general concepts will suffice.
The exact characteristics of EEG signals are, in general terms, unpredictable. This means that one cannot foresee precisely the amplitude of an EEG graphoelement or the duration of an EEG wave. Therefore, it is said that an EEG signal is a realization of a random or stochastic process. Indeed, it is possible to determine some statistical measures of EEG signals that show considerable regularity, such as an average amplitude or an average frequency. This is a general characteristic of random processes, which are characterized by probability distributions and their moments (e.g., mean, variance, skewness, and kurtosis) or by frequency spectra or correlation functions. Such a description of an EEG signal as a realization of a random process implies a mathematical, but not a biophysical, model.
It should be stressed (8) that the biophysical process underlying EEG generation is not necessarily random in nature, but it may have such a high degree of complexity that only a description in statistical terms is justified. Gasser (7) has also emphasized this point; even in the case of signals that are deterministic (e.g., sinusoids) but very complex (e.g., made of many components), a stochastic approach may be the most adequate.
EEG signals are, of course, time series; they are characterized by a set of values as a function of time. An important problem, however, is whether the general methods for analyzing time series can be applied without restrictions to EEG signals.
In Chapter 4, which discusses EEG dynamics, it was mentioned that modern mathematical tools are being used to analyze EEG signals, assuming that signal generation can be described using sets of nonlinear differential equations. These techniques have been developed within the active field of mathematical research called “deterministic chaos.” In essence, nonlinear dynamical systems such as the neuronal networks generating EEG signals can display chaotic behavior; that is, their behavior can become unpredictable for relatively long periods, and EEG signals may be an expression of chaotic behavior. Since new mathematical tools, based on the analysis of complex nonlinear systems such as the correlation dimension, were introduced in EEG, it became clear that EEG signals may be high-dimensional so that in many cases it is difficult, or even impossible, to distinguish whether these signals are generated by random or by high-dimensional nonlinear deterministic processes (9).
SAMPLING, PROBABILITY DISTRIBUTIONS, CORRELATION FUNCTIONS, AND SPECTRA
EEG signals are continuous variations of potential as a function of time. However, in most practical cases where quantitative analysis is applied, signals must be digitized so that they can be processed by digital computer. This means that the EEG signal must be processed in such a way that the random variable, potential as a function of time, will have only one set of discrete values at a set of discrete time instances. In technical terms, the process of analog-to-digital (AD) conversion involves sampling combined with the operation of quantizing. According to definitions commonly used (10), sampling is the “process of obtaining a sequence of instantaneous values of a wave at regular or intermittent intervals” and quantization is the “process in which the continuous range of values of an input signal is divided into nonoverlapping subranges and to each subrange a discrete value of the output is uniquely assigned.”
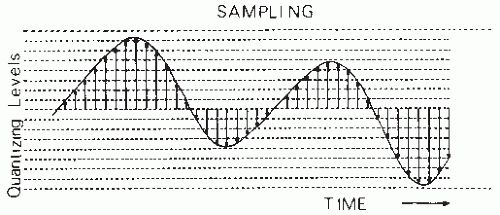
EEG signal sampling must be performed without changing the statistical properties of the continuous signal. Generally, one samples an EEG signal at equidistant time intervals (Δt), thus transforming the continuous signal into a set of impulses with different heights separated by intervals Δt (Fig. 54.1). An important question is the choice of the sampling frequency. This choice is based on the sampling theorem: assuming that a signal x(t) has a frequency spectrum X(f) such that X(f) = 0 for fN, no information is lost by sampling x(t) at equidistant intervals Δt with fN = 1/(2 Δt); fN is called the folding or Nyquist frequency. The sampling frequency, therefore, must be at least equal to 2fN. A consequence of this theorem is that care has to be taken to ensure that the signal to be sampled has no frequency components above fN. Therefore, before sampling, all frequency components greater than fN should be eliminated by low-pass filtering. One should keep in mind that sampling at a frequency below 2fN is not equivalent to filtering; it would produce aliasing or signal distortion due to folding of frequency components larger than fN onto lower frequencies (11). The analog voltages of the signal at the sampling moments are converted to a number corresponding to the amplitude subrange or level. Most EEG analysis can be performed using 512 to 2048 amplitude levels (i.e., 9 to 11 bits). Technical details of AD conversion may be found in Susskind (12) and, for the special case of EEG signals, in Lopes da Silva et al. (11) and Steineberg and Paine (13).
The continuous EEG signal is thus replaced by a string of numbers x(ti) representing the signal amplitude at sequential sample moments; the latter are indicated by the index i along the time axis. The signal is assumed to be a realization of a stationary random process  (ti), which is indicated by underlining the letter (
(ti), which is indicated by underlining the letter ( ). In general, a collection of EEG signals of a certain length recorded under equivalent conditions is available for analysis. The entire collection of EEG signals is called an ensemble; each member of the ensemble is called a sample function or a realization.
). In general, a collection of EEG signals of a certain length recorded under equivalent conditions is available for analysis. The entire collection of EEG signals is called an ensemble; each member of the ensemble is called a sample function or a realization.
 (ti), which is indicated by underlining the letter (
(ti), which is indicated by underlining the letter (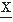 ). In general, a collection of EEG signals of a certain length recorded under equivalent conditions is available for analysis. The entire collection of EEG signals is called an ensemble; each member of the ensemble is called a sample function or a realization.
). In general, a collection of EEG signals of a certain length recorded under equivalent conditions is available for analysis. The entire collection of EEG signals is called an ensemble; each member of the ensemble is called a sample function or a realization.PROBABILITY DISTRIBUTIONS
The digitized EEG signal values x(ti) can be considered realizations of one stochastic variable 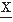 (ti) and may be characterized when stationarity is assumed by a histogram; when in an interval 0 > t > T there are na sample points in the interval a ± 1/2Δ, na/N is called the relative frequency of occurrence of the value a, where N is the total number of samples available. One can define the relative frequencies of all other values similarly. When N becomes infinitely large and Δ infinitely small, na/N will tend to a limit value p(x(ti) = a), called the probability of occurrence of x(ti) = a. The set of values of p(x(ti)) is called the signal probability distribution, characterized by a mean and a number of moments. Considering that the discrete random variable × can take any of a set of values from 1 to M, the mean or average of the sample functions is given as follows (E is the symbol for expectation):
(ti) and may be characterized when stationarity is assumed by a histogram; when in an interval 0 > t > T there are na sample points in the interval a ± 1/2Δ, na/N is called the relative frequency of occurrence of the value a, where N is the total number of samples available. One can define the relative frequencies of all other values similarly. When N becomes infinitely large and Δ infinitely small, na/N will tend to a limit value p(x(ti) = a), called the probability of occurrence of x(ti) = a. The set of values of p(x(ti)) is called the signal probability distribution, characterized by a mean and a number of moments. Considering that the discrete random variable × can take any of a set of values from 1 to M, the mean or average of the sample functions is given as follows (E is the symbol for expectation):
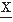 (ti) and may be characterized when stationarity is assumed by a histogram; when in an interval 0 > t > T there are na sample points in the interval a ± 1/2Δ, na/N is called the relative frequency of occurrence of the value a, where N is the total number of samples available. One can define the relative frequencies of all other values similarly. When N becomes infinitely large and Δ infinitely small, na/N will tend to a limit value p(x(ti) = a), called the probability of occurrence of x(ti) = a. The set of values of p(x(ti)) is called the signal probability distribution, characterized by a mean and a number of moments. Considering that the discrete random variable × can take any of a set of values from 1 to M, the mean or average of the sample functions is given as follows (E is the symbol for expectation):
(ti) and may be characterized when stationarity is assumed by a histogram; when in an interval 0 > t > T there are na sample points in the interval a ± 1/2Δ, na/N is called the relative frequency of occurrence of the value a, where N is the total number of samples available. One can define the relative frequencies of all other values similarly. When N becomes infinitely large and Δ infinitely small, na/N will tend to a limit value p(x(ti) = a), called the probability of occurrence of x(ti) = a. The set of values of p(x(ti)) is called the signal probability distribution, characterized by a mean and a number of moments. Considering that the discrete random variable × can take any of a set of values from 1 to M, the mean or average of the sample functions is given as follows (E is the symbol for expectation):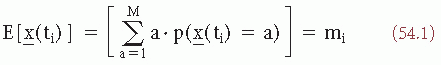
Also definable is a class of statistical functions characteristic of the random process: mn = E[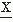 n(ti)] with n = 1, 2, 3, …; these functions are called the nth moments of the discrete random variable
n(ti)] with n = 1, 2, 3, …; these functions are called the nth moments of the discrete random variable 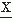 (ti). The implicit assumption here and in the following discussion is that the statistical properties of the signal do not change in the interval T. Therefore, the moments are independent of time ti.
(ti). The implicit assumption here and in the following discussion is that the statistical properties of the signal do not change in the interval T. Therefore, the moments are independent of time ti.
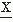 n(ti)] with n = 1, 2, 3, …; these functions are called the nth moments of the discrete random variable
n(ti)] with n = 1, 2, 3, …; these functions are called the nth moments of the discrete random variable 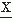 (ti). The implicit assumption here and in the following discussion is that the statistical properties of the signal do not change in the interval T. Therefore, the moments are independent of time ti.
(ti). The implicit assumption here and in the following discussion is that the statistical properties of the signal do not change in the interval T. Therefore, the moments are independent of time ti.The first moment E[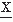 (ti)] is called the mean of
(ti)] is called the mean of 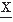 (ti). It is often preferable to consider the central moments (i.e., the moments around the mean); the second central moment is then:
(ti). It is often preferable to consider the central moments (i.e., the moments around the mean); the second central moment is then:
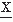 (ti)] is called the mean of
(ti)] is called the mean of 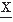 (ti). It is often preferable to consider the central moments (i.e., the moments around the mean); the second central moment is then:
(ti). It is often preferable to consider the central moments (i.e., the moments around the mean); the second central moment is then:Similarly, the third central moment E[(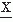 (ti)-(E(
(ti)-(E(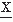 (ti)))3] = m3 can be defined; from this can be derived the skewness factor β1 = m3/(m2)3/2. The fourth central moment is E[(
(ti)))3] = m3 can be defined; from this can be derived the skewness factor β1 = m3/(m2)3/2. The fourth central moment is E[(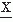 (ti)-(E(
(ti)-(E(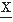 (ti)))4] = m4, from which can be derived the kurtosis excess: β2 = m4/(m2)2. In case of a symmetric amplitude, distribution is β1 = 0; all odd moments are equal to zero. For a gaussian distribution the even moments have specific values, for example, β2 = 3; derivatives from this value indicate the peakedness (β2 > 3) or flatness (β2 < 3) of the distribution (Fig. 54.2).
(ti)))4] = m4, from which can be derived the kurtosis excess: β2 = m4/(m2)2. In case of a symmetric amplitude, distribution is β1 = 0; all odd moments are equal to zero. For a gaussian distribution the even moments have specific values, for example, β2 = 3; derivatives from this value indicate the peakedness (β2 > 3) or flatness (β2 < 3) of the distribution (Fig. 54.2).
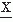 (ti)-(E(
(ti)-(E(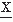 (ti)))3] = m3 can be defined; from this can be derived the skewness factor β1 = m3/(m2)3/2. The fourth central moment is E[(
(ti)))3] = m3 can be defined; from this can be derived the skewness factor β1 = m3/(m2)3/2. The fourth central moment is E[(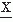 (ti)-(E(
(ti)-(E(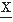 (ti)))4] = m4, from which can be derived the kurtosis excess: β2 = m4/(m2)2. In case of a symmetric amplitude, distribution is β1 = 0; all odd moments are equal to zero. For a gaussian distribution the even moments have specific values, for example, β2 = 3; derivatives from this value indicate the peakedness (β2 > 3) or flatness (β2 < 3) of the distribution (Fig. 54.2).
(ti)))4] = m4, from which can be derived the kurtosis excess: β2 = m4/(m2)2. In case of a symmetric amplitude, distribution is β1 = 0; all odd moments are equal to zero. For a gaussian distribution the even moments have specific values, for example, β2 = 3; derivatives from this value indicate the peakedness (β2 > 3) or flatness (β2 < 3) of the distribution (Fig. 54.2).CORRELATION FUNCTIONS AND SPECTRA
In general terms, successive values of a signal, such as an EEG, which result from a stochastic process are not necessarily independent. On the contrary, it is often found that successive discrete values of an EEG signal have a certain degree of interdependence. To describe this interdependence, one may compute the signal joint probability distribution. As an example, consider the definition of the joint probability applied to a pair of values at two discrete moments, 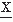 (t1) and
(t1) and 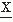 (t2); assume that one disposes of N realizations of the signal; the number of times that at t1 a value v and at t2 a value u are encountered is equal to n12. Thus, the joint probability of
(t2); assume that one disposes of N realizations of the signal; the number of times that at t1 a value v and at t2 a value u are encountered is equal to n12. Thus, the joint probability of 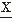 (t1) and
(t1) and 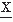 (t2) = u may be defined as follows:
(t2) = u may be defined as follows:
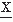 (t1) and
(t1) and 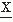 (t2); assume that one disposes of N realizations of the signal; the number of times that at t1 a value v and at t2 a value u are encountered is equal to n12. Thus, the joint probability of
(t2); assume that one disposes of N realizations of the signal; the number of times that at t1 a value v and at t2 a value u are encountered is equal to n12. Thus, the joint probability of 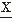 (t1) and
(t1) and 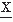 (t2) = u may be defined as follows:
(t2) = u may be defined as follows:A complete description of the properties of the signal generated by a random process can be achieved by specifying the joint probability density function:
for every choice of the discrete time samples t1, t2,…, tn and for every finite value of n. The computation of this function, however, is rather complex. A simpler alternative to this form of description is to compute a number of averages characteristic of the signal, such as convariance, correlations, and spectra. These averages do not necessarily describe a stochastic signal completely, but they may be very useful for a general description of signals such as EEG.
The convariance between two random variables at two time samples 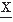 (t1) and
(t1) and 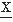 (t2) is given by the following expectation:
(t2) is given by the following expectation:
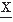 (t1) and
(t1) and 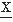 (t2) is given by the following expectation:
(t2) is given by the following expectation:Estimating the covariance between any two variables 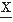 (t1) and
(t1) and 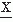 (t2) requires averaging over a umber of realizations of an ensemble. Another way to estimate the convariance, provided that the signal is stationary and ergodic (for a discussion of these concepts see Ref. 14), is by computing a time average, for one realization of the signal, of the product of the signal and a replica of itself shifted by a certain time τk along the time axis. This time average is called the autocorrelation function:
(t2) requires averaging over a umber of realizations of an ensemble. Another way to estimate the convariance, provided that the signal is stationary and ergodic (for a discussion of these concepts see Ref. 14), is by computing a time average, for one realization of the signal, of the product of the signal and a replica of itself shifted by a certain time τk along the time axis. This time average is called the autocorrelation function:
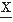 (t1) and
(t1) and 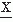 (t2) requires averaging over a umber of realizations of an ensemble. Another way to estimate the convariance, provided that the signal is stationary and ergodic (for a discussion of these concepts see Ref. 14), is by computing a time average, for one realization of the signal, of the product of the signal and a replica of itself shifted by a certain time τk along the time axis. This time average is called the autocorrelation function:
(t2) requires averaging over a umber of realizations of an ensemble. Another way to estimate the convariance, provided that the signal is stationary and ergodic (for a discussion of these concepts see Ref. 14), is by computing a time average, for one realization of the signal, of the product of the signal and a replica of itself shifted by a certain time τk along the time axis. This time average is called the autocorrelation function: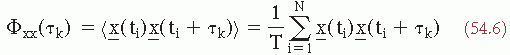
where τk = k·Δt.
The following description considers continuous random variables x(t), for the sake of simplifying the formulas. Assuming that every sample function, or realization, is representative of the whole signal being analyzed, it can be shown that for stationary and ergodic processes the time average Φxx(τ) for one realization 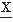 (t) is an estimate of the ensemble average Rxx(τ):
(t) is an estimate of the ensemble average Rxx(τ):
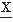 (t) is an estimate of the ensemble average Rxx(τ):
(t) is an estimate of the ensemble average Rxx(τ):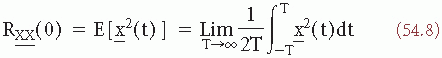
which is the signal’s average power or variance σ. An important property of the autocorrelation function is that its Fourier transform (FT) is:
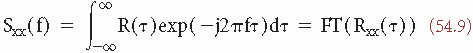
Sxx(f) is called the power density spectrum, or simply the power spectrum, a common method of EEG quantification (Fig. 54.3). The power spectrum Sxx(f) is a function of frequency (Hz); it gives the distribution of the squared amplitude of different frequency components. It should be noted that the word power does not have the meaning of dissipated power in an RC circuit but is used here in another sense. This discussion deals with a question of time series analysis. In general, a stochastic
time function may be expressed in one of the several ways, as a voltage, a length, a velocity, a number of occurrences of a certain event, and so forth. The power spectrum or simply the spectral density of the time function is the FT of the autocorrelation function, the dimension of which is the function’s amplitude dimension squared. In case the signal dimension is in volts, the power spectrum is in (V2·sec) or (V2/Hz). Of course, if the function’s amplitude is in any other dimension, the intensity of the corresponding power spectrum would be yet another dimension. It is useful to keep a clear distinction between electric power dissipated in an electric circuit (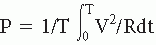 with units [V2·sec/Ω]) and power spectrum.
with units [V2·sec/Ω]) and power spectrum.
time function may be expressed in one of the several ways, as a voltage, a length, a velocity, a number of occurrences of a certain event, and so forth. The power spectrum or simply the spectral density of the time function is the FT of the autocorrelation function, the dimension of which is the function’s amplitude dimension squared. In case the signal dimension is in volts, the power spectrum is in (V2·sec) or (V2/Hz). Of course, if the function’s amplitude is in any other dimension, the intensity of the corresponding power spectrum would be yet another dimension. It is useful to keep a clear distinction between electric power dissipated in an electric circuit (
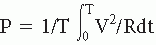 with units [V2·sec/Ω]) and power spectrum.
with units [V2·sec/Ω]) and power spectrum.A function that represents the average correlation between two signals  (t) and
(t) and 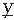 (t) may be defined in terms equivalent to expression 54.7:
(t) may be defined in terms equivalent to expression 54.7:
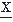 (t) and
(t) and 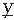 (t) may be defined in terms equivalent to expression 54.7:
(t) may be defined in terms equivalent to expression 54.7:where the signals 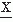 (t) and
(t) and 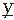 (t) are assumed to have means of zero. Rxy(τ) measures the correlation between the two signals and is called the cross-correlation function. Similarly, one can define the FT of Rxy, which is the cross-power spectrum between signals
(t) are assumed to have means of zero. Rxy(τ) measures the correlation between the two signals and is called the cross-correlation function. Similarly, one can define the FT of Rxy, which is the cross-power spectrum between signals 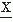 and
and 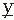 :
:
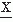 (t) and
(t) and 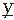 (t) are assumed to have means of zero. Rxy(τ) measures the correlation between the two signals and is called the cross-correlation function. Similarly, one can define the FT of Rxy, which is the cross-power spectrum between signals
(t) are assumed to have means of zero. Rxy(τ) measures the correlation between the two signals and is called the cross-correlation function. Similarly, one can define the FT of Rxy, which is the cross-power spectrum between signals 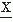 and
and 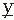 :
:Fundamental discussions of power spectra and related topics are found in many textbooks on signal analysis, for example, Refs. 15 and 14. This discussion cannot go into details about ways of Bendat and Piersol (16) and Otnes and Enochson (17). Application of the frequency analysis principle to EEG signal analysis has a long history, beginning with the pioneering work of Dietsch (18), Grass and Gibbs (19), Knott and Gibbs (20), Drohocki (21), and Walter (22,23). Brazier and Casby (24) and Barlow and Brazier (25) first computed the autocorrelation functions of EEG signals. The general principles on which this work has been based have remained essentially the same since Wiener proposed these signal analysis methods (for a review, see Ref. 26). An important advance in computing power spectra has been achieved with the introduction of a new algorithm for computing the discrete Fourier transform, known as the fast Fourier transform (FFT) (27). In this case, it is assumed that one wants to compute the power spectrum of a discrete EEG signal; the epoch [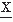 (t1)] is considered as a signal sampled at intervals Δt, x(n Δt) with a total of N samples (n = 1…N). By using the discrete FT, the so-called periodogram F(fi) can be computed:
(t1)] is considered as a signal sampled at intervals Δt, x(n Δt) with a total of N samples (n = 1…N). By using the discrete FT, the so-called periodogram F(fi) can be computed:
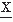 (t1)] is considered as a signal sampled at intervals Δt, x(n Δt) with a total of N samples (n = 1…N). By using the discrete FT, the so-called periodogram F(fi) can be computed:
(t1)] is considered as a signal sampled at intervals Δt, x(n Δt) with a total of N samples (n = 1…N). By using the discrete FT, the so-called periodogram F(fi) can be computed: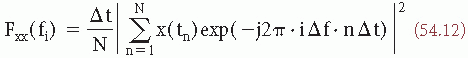
where fi = i · Δf with i = 0, 1, 2, …, N. The periodogram can be smoothed by means of a window W(fk) in order to obtain Pxx(fk), which is a better estimate of the real power spectrum Sxx(f):
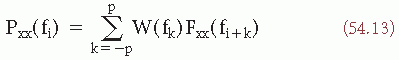
where W(fk) is the smoothing window with a duration of (2p + 1) samples or data points. Similarly, one can compute a smoothed estimate of the cross-power spectrum (Sxy), which might be called Cxy(f).
The FFT power spectral analysis and its applications are discussed in more detail below.
The close relationship between the concepts of variance σ2, autocorrelation (equations 54.6 and 54.7), and power density spectrum (equation 54.9) has already been made apparent; in fact Rxx(0) = σ2 and
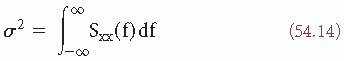
The autocorrelation function R(τ) and the power density spectrum S(f) correspond thus to the second-order moment of the probability distribution of the random process.
In case the signals are not gaussian, higher order spectra moments must be considered. These can be derived as follows. Assuming that the signal has mean = 0, one can write (as in expression 54.7):
Similar to expression 54.9, the two-dimensional Fourier transform FT2 of Rxx(τ1, τ2) can be defined as the bispectrum or bispectral density:
This discussion cannot go into details about ways of estimating the bispectrum Bxx. For a detailed account of bispectral EEG analysis, refer to Huber et al. (28) and to Dumermuth et al. (29). It is, however, interesting to note that high Bxx values for a couple of frequencies, f1 and f2, indicate phase coupling within the frequency triplet f1, f2, and (f1 + f2). The third moment of the probability distribution, or skewness, is related to the bispectrum. When there exists a sufficiently strong relation between two harmonically related frequency components in a signal, there will exist a significant bispectrum and skewness. The process in such a case is not gaussian; if it were gaussian with mean zero, the bispectrum would be zero. The bispectrum can be used to determine whether the system underlying the EEG generation has nonlinear properties. An example of this form of analysis is given in Figure 54.4.
This section has demonstrated the progression from the basic principles of probability distribution and corresponding moments to the concepts of autocorrelation, power spectra, and high-order spectra. It is also of interest to examine the moments of the spectral density Sxx(f), because this analysis leads to another set of concepts applicable to EEG analysis, the so-called descriptors of Hjorth (30). Thus, one can define the nth spectral moment as follows:
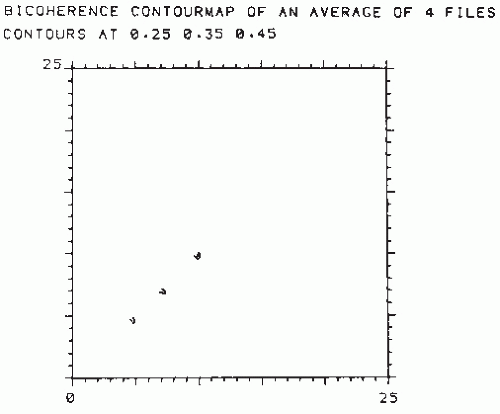 Figure 54.4 Contour map of the normalized bispectrum (also called bicoherence) of an EEG signal recorded from a subject who presented an alpha variant (the corresponding power spectrum is shown in Fig. 54.8). The plot shows three maxima in the value of bicoherence (>0.25). One is at the intersection of approximately 5 and 5 Hz (phase coupling between 5, 5, and 10 Hz); another one is at the intersection of about 7 and 7 Hz (phase coupling between 7, 7, and 14 Hz). Still another is at the intersection of about 10 and 10 Hz (phase coupling between 10, 10, and 20 Hz). This means that the two peaks seen in the power spectrum of Figure 54.8 at 5 and 10 Hz, respectively, are harmonically related, that is, 5 Hz is one-half subharmonic of the dominant alpha frequency. Moreover, there is another component at 20 Hz, difficult to see in the power spectrum, of Figure 54.8, which is also harmonically related to the alpha frequency (i.e., a second harmonic of the alpha component is also present). Another component at about 7 Hz related to 14 Hz can also be identified. (This component may be distinguished as a small notch at the flank of the 10-Hz peak in the power spectrum of Fig. 54.8.) |
The zero-order moment is then:
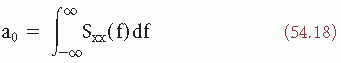
which is equal to the variance σ2.
It can be shown (for derivation, see Ref. 31) that the second-order moment is defined by the following expression:
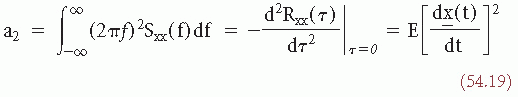
and the fourth-order moment is:
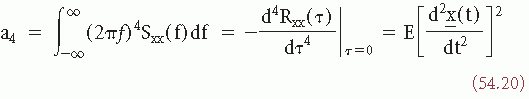
INTERVAL OR PERIOD ANALYSIS
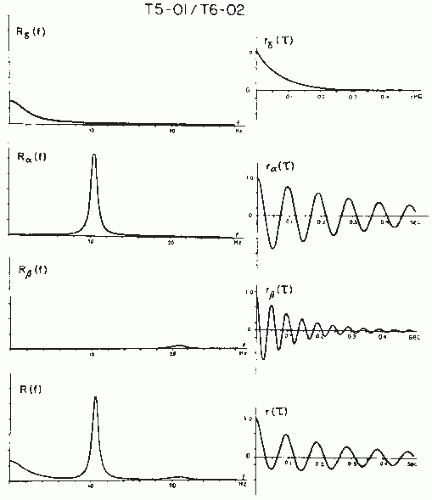
An alternative method of EEG signal analysis is based on measuring the distribution of intervals between zero and other level crossings, or between maxima and minima.
A level crossing may be defined in general terms as the time at which a signal 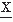 (t) passes a certain amplitude level b; b = 0 is a special case referred to as zero crossing (Fig. 54.5). Knowledge of the probability density function of the intervals between successive zero crossings can be useful in characterizing some statistical properties of the signal
(t) passes a certain amplitude level b; b = 0 is a special case referred to as zero crossing (Fig. 54.5). Knowledge of the probability density function of the intervals between successive zero crossings can be useful in characterizing some statistical properties of the signal 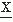 (t) (mean value 0). p0(τ) can be called the probability distribution density function of the intervals between any two successive zero crossings and p1(τ), corresponding to the total time τ between successive zero crossings at which the signal changes in the same direction (i.e., from positive to negative or vice versa). In practice, these functions can be approximated by computing histograms of the interval length between two successive zero crossings or between zero crossings at which the signal has a derivative with the same sign. The moments of the distribution function can also be computed; the simplest case is to compute the average number of zero crossings per time unit (N0) (e.g., per second) of the signal
(t) (mean value 0). p0(τ) can be called the probability distribution density function of the intervals between any two successive zero crossings and p1(τ), corresponding to the total time τ between successive zero crossings at which the signal changes in the same direction (i.e., from positive to negative or vice versa). In practice, these functions can be approximated by computing histograms of the interval length between two successive zero crossings or between zero crossings at which the signal has a derivative with the same sign. The moments of the distribution function can also be computed; the simplest case is to compute the average number of zero crossings per time unit (N0) (e.g., per second) of the signal 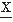 (t):
(t):
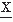 (t) passes a certain amplitude level b; b = 0 is a special case referred to as zero crossing (Fig. 54.5). Knowledge of the probability density function of the intervals between successive zero crossings can be useful in characterizing some statistical properties of the signal
(t) passes a certain amplitude level b; b = 0 is a special case referred to as zero crossing (Fig. 54.5). Knowledge of the probability density function of the intervals between successive zero crossings can be useful in characterizing some statistical properties of the signal 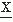 (t) (mean value 0). p0(τ) can be called the probability distribution density function of the intervals between any two successive zero crossings and p1(τ), corresponding to the total time τ between successive zero crossings at which the signal changes in the same direction (i.e., from positive to negative or vice versa). In practice, these functions can be approximated by computing histograms of the interval length between two successive zero crossings or between zero crossings at which the signal has a derivative with the same sign. The moments of the distribution function can also be computed; the simplest case is to compute the average number of zero crossings per time unit (N0) (e.g., per second) of the signal
(t) (mean value 0). p0(τ) can be called the probability distribution density function of the intervals between any two successive zero crossings and p1(τ), corresponding to the total time τ between successive zero crossings at which the signal changes in the same direction (i.e., from positive to negative or vice versa). In practice, these functions can be approximated by computing histograms of the interval length between two successive zero crossings or between zero crossings at which the signal has a derivative with the same sign. The moments of the distribution function can also be computed; the simplest case is to compute the average number of zero crossings per time unit (N0) (e.g., per second) of the signal 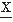 (t):
(t):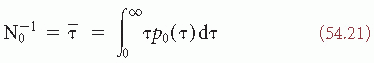
This means that the number of zero crossings per time unit N0 equals the reciprocal of the mean interval length τ.
In some cases it is helpful to determine the probability density function of the intervals between two adjacent zero crossings where the sign of 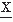 (t) changes from negative to positive or vice versa. In this case, it is necessary to compute additionally the zero crossing interval distribution of the first derivative of
(t) changes from negative to positive or vice versa. In this case, it is necessary to compute additionally the zero crossing interval distribution of the first derivative of 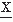 (t),
(t), 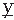 (t) (i.e.,
(t) (i.e., 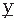 (t) = d
(t) = d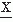 (t)/dt). If the signal
(t)/dt). If the signal 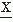 (t) to be analyzed is quasi-stationary and has a gaussian distribution, a mathematical relation between Nk, the average rate of zero crossings of the kth derivative of
(t) to be analyzed is quasi-stationary and has a gaussian distribution, a mathematical relation between Nk, the average rate of zero crossings of the kth derivative of 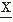 (t), and the power spectrum Sxx(f) can be shown (32, 33 and 34):
(t), and the power spectrum Sxx(f) can be shown (32, 33 and 34):
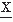 (t) changes from negative to positive or vice versa. In this case, it is necessary to compute additionally the zero crossing interval distribution of the first derivative of
(t) changes from negative to positive or vice versa. In this case, it is necessary to compute additionally the zero crossing interval distribution of the first derivative of 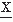 (t),
(t), 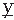 (t) (i.e.,
(t) (i.e., 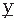 (t) = d
(t) = d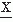 (t)/dt). If the signal
(t)/dt). If the signal 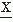 (t) to be analyzed is quasi-stationary and has a gaussian distribution, a mathematical relation between Nk, the average rate of zero crossings of the kth derivative of
(t) to be analyzed is quasi-stationary and has a gaussian distribution, a mathematical relation between Nk, the average rate of zero crossings of the kth derivative of 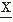 (t), and the power spectrum Sxx(f) can be shown (32, 33 and 34):
(t), and the power spectrum Sxx(f) can be shown (32, 33 and 34):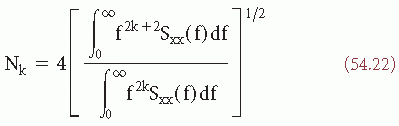
In interval analysis, only the values Nk for k = 0, 1, 2 are usually computed. N0 thus represents the average rate of zero crossings of d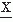 (t)/dt (i.e., the rate of intervals between extremes of the signal
(t)/dt (i.e., the rate of intervals between extremes of the signal 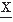 (t)); N2 represents the average rate of zero crossings of d2
(t)); N2 represents the average rate of zero crossings of d2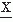 (t)/dt2 (i.e., the rate of intervals of the a nonparametric or a parametric approach that is combined inflection points of
(t)/dt2 (i.e., the rate of intervals of the a nonparametric or a parametric approach that is combined inflection points of 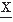 (t)).
(t)).
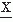 (t)/dt (i.e., the rate of intervals between extremes of the signal
(t)/dt (i.e., the rate of intervals between extremes of the signal 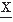 (t)); N2 represents the average rate of zero crossings of d2
(t)); N2 represents the average rate of zero crossings of d2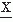 (t)/dt2 (i.e., the rate of intervals of the a nonparametric or a parametric approach that is combined inflection points of
(t)/dt2 (i.e., the rate of intervals of the a nonparametric or a parametric approach that is combined inflection points of 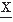 (t)).
(t)).It can be shown (32) that expression 54.22 can separately also be given in terms of the autocorrelation function:
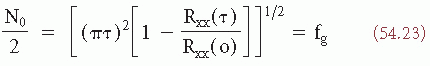
where fg is the so-called gyrating frequency (35).
These relations between the number of zero crossings per time unit and either spectral moments or the autocorrelation function for EEG signals have been studied in detail by Saltzberg and Burch (36), who concluded that, when the purpose is to monitor long-term changes in the statistical properties of EEG signals, it is legitimate to use average zero-crossing rates to calculate moments of the power spectral density.
Instead of measuring intervals between zero crossings, one can characterize a signal by determining intervals between successive maxima (or minima), which defines a “wave,” or between a maximum and the immediately following minimum or vice versa, which defines a “half-wave.” The section “Mimetic Analysis” considers some of the variants of interval analysis as applied to EEG signals; the straightforward applications of interval analysis are described in the section “Time-Frequency Analysis.”
EEG SIGNAL PROCESSING METHODS IN PRACTICE
The previous section considered the statistical properties of EEG signals as realizations of random processes, explaining how such signals can be characterized by the corresponding probability distribution and its moments, by the autocorrelation function or the power spectrum, or by distribution of intervals between level crossings. In all cases, the EEG was treated as a stochastic signal without a specific generation model. Therefore, all the previously described methods and related ones are nonparametric methods. Parametric methods may also be used to analyze EEG signals; in such cases one assumes the EEG signal to be generated by a specific model. For example, assuming that the EEG signal is the output of a linear filter given a white noise input allows characterization of the linear filter by a set of coefficients or parameters (e.g., it may correspond to an autoregressive model as explained below).
Therefore, EEG analysis methods can be divided into two basic categories, parametric and nonparametric. Such a division is conceptually more correct than the more common differentiation between frequency and time domain methods because, as has been explained, such methods as power spectra in the frequency domain and interval analysis in the time domain are closely related; indeed, they represent two different ways of describing the same phenomena. The methods of EEG analysis described here are classified as shown in Table 54.1.
Not all EEG analysis methods can be assigned to one of the two general categories just described. Those having mixed character (i.e., methods that have, as a starting point, a nonparametric or parametric approach that is combined with pattern recognition techniques) must be considered separately. The latter fall into the category of pattern recognition methods. Last, this section shall discuss topographic analysis methods, in which the emphasis is on topographic relations between derivations. Not included here are the evoked potentials, which are discussed elsewhere.
A thorough review of the main techniques currently in use in EEG analysis has been edited by Gevins and Remond (37). For more details on methods of analyzing brain electric signals, the reader is referred to this authoritative handbook.
Table 54.1 EEG Analysis Methods | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
NONPARAMETRIC METHODS
Amplitude Distribution
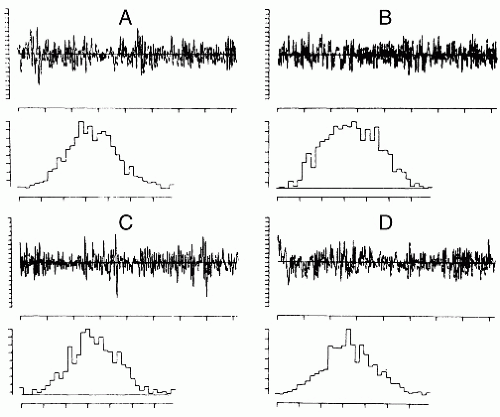
A random signal can be characterized by the distribution of amplitude and its moments. An example of an amplitude distribution is shown in Figure 54.2. The first question that is asked regarding the amplitude distribution of an EEG epoch is whether the distribution is normal or gaussian. The most common tests of normality are the chi-square goodness-of-fit test (17), the Kolmogorov-Smirnov test, or the values of skewness and kurtosis (7,38). It has been shown (39) that, for the small EEG samples usually analyzed, the Kolmogorov-Smirnov test is more powerful than the chi-square test. It should be emphasized that in order to apply these tests of goodness-of-fit, two requirements must be satisfied: stationarity and independence of adjacent samples. The first requirement was considered in the previous sections. The second requirement is a well-known prerequisite for the application of the statistical tests of the type we consider here. Persson (40) has clearly pointed out the pitfalls of applying goodness-of-fit tests to EEG amplitude distributions. The problem is that the EEG signals are usually recorded at such a sampling rate that, depending on the spectral composition of the signal, adjacent samples are more or less correlated. In this way, the second requirement is commonly violated. This has also been shown clearly by McEwen and Anderson’s (5) statistical study of EEG signals. The degree of correlation between adjacent samples can be deduced from the autocorrelation function. Persson found that a correlation coefficient of 0.50 or larger for adjacent samples introduces a considerable error in interpreting a goodness-of-fit test. His experience with EEG signals led to the conclusion that sampling rates in most cases should be restricted to about 20/sec in order to achieve an acceptably small degree of correlation between adjacent samples.
It is of general interest to know an EEG sample’s type of amplitude distribution. Several studies have been carried out, mainly investigating whether or not EEG amplitude distributions were gaussian. Saunders (41), using a sample rate of 60/sec, epoch lengths of 8.33 seconds, and the chi-square test, concluded that alpha activity had a gaussian distribution; this confirmed previous results from Lion and Winter (42) and Kozhevnikov (43), who used analog techniques. On the contrary, Campbell et al. (44), using a sample rate of 125/sec, epoch lengths of 52.8 seconds, and the chi-square test, concluded that most EEG signals had non-gaussian distributions; however, it is likely that in this case the dual requirements of stationarity and independence were not met.
The results obtained by Elul (45) are of special interest because he examined EEG time-varying properties using amplitude distributions for epochs of 2 seconds (200 samples/sec, chi-square goodness-of-fit test); this study most certainly failed to meet the requirement of independence. Nevertheless, Elul found that a resting EEG signal could be considered to have a gaussian distribution 66% of the time, whereas, during performance of a mental arithmetic task, this incidence decreased to 32%. Evaluating a small series of waking EEGs in twins, Dumermuth (46,47) found amplitude distribution deviations from gaussianity in the majority of the subjects; he tested the normality hypothesis by way of the third- and fourth-order moments, skewness, and kurtosis. In adult sleep EEG, skewness and kurtosis also deviated significantly from the values expected for a gaussian distribution depending on sleep stage (48,49). These observations have led to a study of higher order moments of the spectral density function using bispectral analysis.
The method recommended to test whether EEG amplitude distributions are gaussian is that proposed by Gasser (7,38); it involves calculating skewness and kurtosis after correction in view of the possibility that adjacent samples may have a large (e.g., >0.50) degree of correlation. The allowed kurtosis and skewness values can be found in statistical tables. Kurtosis in most cases without paroxysmal activity or artifacts is within the limits allowed to accept the normality hypothesis; skewness different from zero is encountered particularly in those cases in which harmonic components are present in the power spectra. In such instances, the bispectrum exists (see below).
An alternative method of calculating measures of EEG amplitude was developed by Drohocki (50) and is used mainly in psychopharmacologic and psychiatric studies (see review in Ref. 51). This method involves measuring the surface of rectified EEG waves. Its usefulness for routine EEG analysis is limited.
Interval Analysis
Interval or period analysis has been used, as described above, to study the statistical properties of EEG signals in general and in relation to other analysis methods, such as autocorrelation functions and power spectra. This discussion considers a more practical aspect, the simplicity of evaluating EEG signals using interval analysis. The method, as originally applied by Saltzberg et al. (52) and Burch et al. (53), has been shown to be useful primarily in quantifying EEG changes induced by psychoactive drugs (54, 55, 56 and 57), monitoring long-term EEG changes during anesthesia (58,59), psychiatry (60), and sleep research (see Ref. 35).
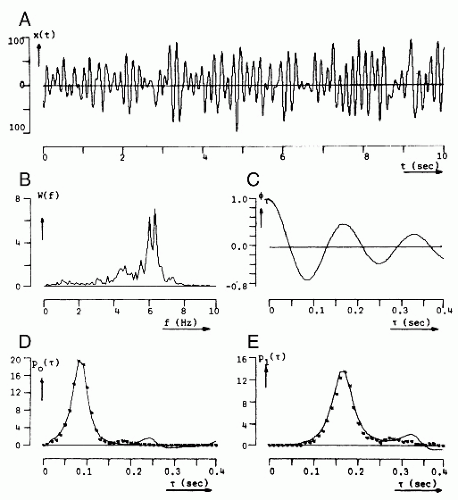
When using interval analysis, it is good practice to compute not only the zero crossings of the original EEG signal, but also those of the signal’s first and second derivatives, to obtain more information about the spectral properties of the signal. One disadvantage of this method is sensitivity to high-frequency noise in the estimation of zero crossings. This problem can be avoided by introducing hysteresis, that is, by creating a dead band (e.g., between +a and −a µV) so that no zero crossing can be detected when the signal has an amplitude between those limits. In this way, Pronk et al. (58) have found that a dead band between + 3 and −3 µV is a good practical choice. Another disadvantage is that, when examining histograms of zero-crossing counts, it is easy to underestimate the contribution of low-frequency components, of which there may be very few, and to overestimate fast frequency components. These disadvantages are particularly evident when zero-crossing histograms and power spectra of the same signal are compared as shown in Figure 54.6 (61). Sometimes corrections are made to enhance the number of long intervals in relation to the short ones, but this may complicate the interpretations even more.
Another approach is to compute zero-crossing intervals only within determined frequency bands; this may solve the problem of missing superimposed waves (62,63).
The main advantage of zero-crossing analysis is ease of computation, which makes this method particularly attractive for the online quantification of very long EEG records, for example, during sleep or intensive monitoring. To perform interval analysis, it is useful to combine it with prefiltering (31) in the analysis of narrow-band signals.
Interval-Amplitude Analysis
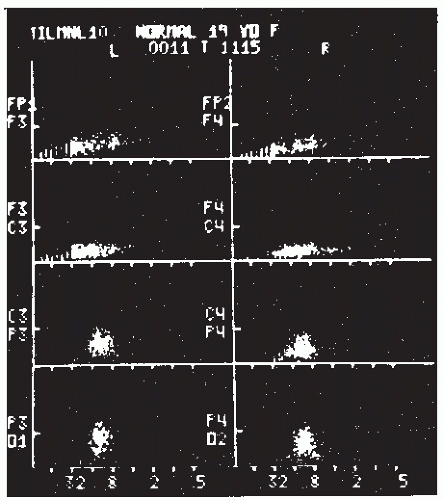
Interval-amplitude analysis is the method by which the EEG is decomposed in waves or half-waves, defined both in time, by the interval between zero crossings, and in amplitude by the peak-to-trough amplitudes. This hybrid method had been proposed repeatedly in the past by Marko and Petsche (64), Leader et al. (65), Legewie and Probst (62), and Pfurtscheller and Koch (66); it has been applied intensively in a clinical setting by Harner (67) and Harner and Ostergren (68). The latter called this method “sequential analysis” because the amplitude and interval duration of successive half-waves are analyzed, displayed, and stored in sequence in real time. The method used by these authors requires that the sampling rate be at least 250/sec, the zero level be updated continuously by estimating the running mean zero level, and, as just discussed, there be a dead band to avoid the influence of high-frequency noise. The high-frequency sampling is desirable in order to obtain a relatively accurate estimate of the peaks and troughs. The amplitude and the interval duration of a half-wave are defined by the peak-trough differences in amplitude and time; the amplitude and the interval duration of a wave are defined by the mean amplitude and the sum of the interval durations of two consecutive half-waves. These data are displayed in a scatter diagram as illustrated in Figure 54.7.
Correlation Analysis
In practical terms, the computation of correlation functions in the 1950s and 1960s constituted the forerunner of contemporary spectral analysis of EEG signals (25,69,70) and provided an impetus to implement EEG quantification in practice. However, the computations were time-consuming and therefore not widely used. A simplified form of correlator was introduced, based on the fact that auto- or cross-correlation functions can be approximated by replacing the signals 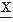 (t) and
(t) and 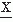 (t + τ) (see equation 54.4) by their signs (sign x(t) and sign x(t + τ), where sign x(t) = +1 for x(t) > 0 and sign x(t) = −1 for x(t) ≤ 0), as demonstrated by McFadden (71). The function thus defined is called the polarity coincidence correlation function, and it has proved useful in EEG analysis (72, 73 and 74). Another simplified form of EEG analysis that is akin to correlation has been used by Kamp et al. (75) and Lesèvre and Remond (76). It can be called autoaveraging and consists of making pulses at a certain phase of the EEG (e.g., zero crossing, peak, or trough) that are then used to trigger a device that averages the same signal (autoaveraging) or another signal (cross-averaging). In this way, rhythmic EEG phenomena can be detected and some characteristic measures obtained.
(t + τ) (see equation 54.4) by their signs (sign x(t) and sign x(t + τ), where sign x(t) = +1 for x(t) > 0 and sign x(t) = −1 for x(t) ≤ 0), as demonstrated by McFadden (71). The function thus defined is called the polarity coincidence correlation function, and it has proved useful in EEG analysis (72, 73 and 74). Another simplified form of EEG analysis that is akin to correlation has been used by Kamp et al. (75) and Lesèvre and Remond (76). It can be called autoaveraging and consists of making pulses at a certain phase of the EEG (e.g., zero crossing, peak, or trough) that are then used to trigger a device that averages the same signal (autoaveraging) or another signal (cross-averaging). In this way, rhythmic EEG phenomena can be detected and some characteristic measures obtained.
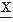 (t) and
(t) and 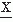 (t + τ) (see equation 54.4) by their signs (sign x(t) and sign x(t + τ), where sign x(t) = +1 for x(t) > 0 and sign x(t) = −1 for x(t) ≤ 0), as demonstrated by McFadden (71). The function thus defined is called the polarity coincidence correlation function, and it has proved useful in EEG analysis (72, 73 and 74). Another simplified form of EEG analysis that is akin to correlation has been used by Kamp et al. (75) and Lesèvre and Remond (76). It can be called autoaveraging and consists of making pulses at a certain phase of the EEG (e.g., zero crossing, peak, or trough) that are then used to trigger a device that averages the same signal (autoaveraging) or another signal (cross-averaging). In this way, rhythmic EEG phenomena can be detected and some characteristic measures obtained.
(t + τ) (see equation 54.4) by their signs (sign x(t) and sign x(t + τ), where sign x(t) = +1 for x(t) > 0 and sign x(t) = −1 for x(t) ≤ 0), as demonstrated by McFadden (71). The function thus defined is called the polarity coincidence correlation function, and it has proved useful in EEG analysis (72, 73 and 74). Another simplified form of EEG analysis that is akin to correlation has been used by Kamp et al. (75) and Lesèvre and Remond (76). It can be called autoaveraging and consists of making pulses at a certain phase of the EEG (e.g., zero crossing, peak, or trough) that are then used to trigger a device that averages the same signal (autoaveraging) or another signal (cross-averaging). In this way, rhythmic EEG phenomena can be detected and some characteristic measures obtained.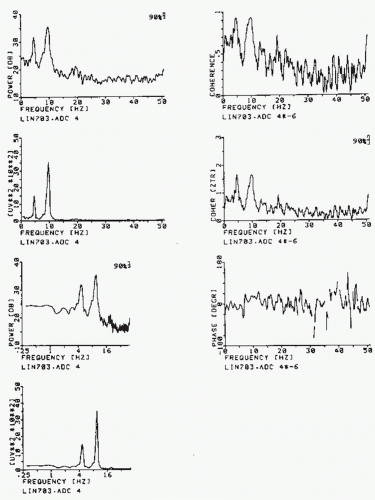 Figure 54.8 Left-hand column: Different ways of plotting the spectrum of the same EEG epoch, the bicoherence of which is shown in Figure 54.4. First plot: y-axis, power in dB, and x-axis, frequency (Hz) along a linear scale; the 90% confidence band of the spectral estimate is indicated. Second plot: y-axis, power in µV2/Hz, and x-axis as above. Third plot: y-axis, power in dB, and x-axis, frequency (Hz) logarithmic scale (this way emphasizes somewhat the low-frequency components). Fourth plot: y-axis, power in µV2/Hz, and x-axis, frequency (Hz) along a logarithmic scale. Right-hand column: First plot: squared coherence (Coh or (γ2)) between two symmetric EEG signals; the power of one is shown in the plots on the left side. Second plot: the same function as above; along the vertical axis the z transformed coherence is plotted, z = (1/2)ln((1 + γ)/(1 – γ)); the advantage of this form of presentation lies in the fact that, in this case, the confidence bands are the same for the whole curve and are not dependent on the value of 2. Third plot: phase spectrum corresponding to the coherence spectrum shown above. |
However, correlation analysis has lost much of its attractiveness for EEG analysts since the advent of FT computation of power spectra. The latter technique is less time-consuming and therefore more economical, and, in general terms, more powerful. Above all, it is difficult to determine from an autocorrelation function EEG components when the signals contain more than one dominant rhythm, an investigation that can be done simply by using the power spectrum (Fig. 54.8). Nevertheless, it should be noted that the simplified methods of correlation analysis just described and used in the 1960s can still have practical value in simple problems, such as computing an alpha average.
The computation of autocorrelation functions has been revived due to the introduction of such parametric analysis methods as the autoregressive model, which, as described below, implies the computation of such functions. Michael and Houchin (77) have even proposed a method of segmenting EEG signals based on the autocorrelation function.
Related to correlation functions is the method of complex demodulation (78). With this method, a particular frequency component (e.g., ˜10 Hz) can be detected and followed as a function of time. In this case, a priori knowledge of the component to be
analyzed is necessary. Assuming, thus, that in an EEG signal a component at about 10 Hz exists and should be followed, one can set an “analysis oscillator” at 10 Hz; the oscillator output and the signal are then multiplied. The product contains components at the sum frequency (˜20 Hz) and at the difference frequency (˜0 Hz). This product is smoothed so that only the difference components (at about 0 Hz) are considered. In this way, phase and amplitude of EEG frequency components can be detected and their modulation in time determined. Complex demodulation has been used to analyze rhythmic components of visual potentials (79) and sleep spindles (80). This method is similar to a direct Fourier analysis in which an EEG signal is multiplied by sines and cosines at a particular frequency in the study of evoked potentials (81) and also the method of phase-locked loop analysis as used to detect sleep spindles (82,83).
analyzed is necessary. Assuming, thus, that in an EEG signal a component at about 10 Hz exists and should be followed, one can set an “analysis oscillator” at 10 Hz; the oscillator output and the signal are then multiplied. The product contains components at the sum frequency (˜20 Hz) and at the difference frequency (˜0 Hz). This product is smoothed so that only the difference components (at about 0 Hz) are considered. In this way, phase and amplitude of EEG frequency components can be detected and their modulation in time determined. Complex demodulation has been used to analyze rhythmic components of visual potentials (79) and sleep spindles (80). This method is similar to a direct Fourier analysis in which an EEG signal is multiplied by sines and cosines at a particular frequency in the study of evoked potentials (81) and also the method of phase-locked loop analysis as used to detect sleep spindles (82,83).
Power Spectra Analysis
A classical way of describing an EEG signal is in terms of frequency as established by the common EEG frequency bands. It is possible to obtain information on the frequency components of EEG signals using interval or period analysis. However, the most appropriate methods in this respect are analog filtering or Fourier analysis, using either expression 54.9 (i.e., the FT of the autocorrelation function) or expressions 54.12 and 54.13 (i.e., the periodogram). Several forms of analog filtering were introduced in the early days of EEG research; that technique reached a technical level appropriate for clinical application mainly due to the work of Walter (22,23). Even in the 1960s banks of active analog filters were used to decompose EEG signals into frequency components (84, 85, 86 and 87). In 1975, Matousek and collaborators compared analog and digital techniques of EEG spectral analysis and demonstrated clearly the superiority of digital techniques. Digital methods are more accurate and flexible; using digital computers simplifies multichannel analysis.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree